An automorphic form is a kind of function of the adelic points (see also Adeles and Ideles) of a reductive group (see also Reductive Groups Part I: Over Algebraically Closed Fields), that can be used to investigate its representation theory. Choosing an important kind of function of a group that will be helpful in investigating its representation theory was also discussed in Representation Theory and Fourier Analysis, where we found the square-integrable functions on the circle to be useful in studying its representations (or that of the real line) since it decomposed into a direct sum of irreducible representations. In fact, the cuspidal automorphic forms we will introduce later on in this post will also have this property (called semisimple) of decomposing into a direct sum of irreducible representations.
Remark: We have briefly mentioned, in the unramified case, cuspidal automorphic forms as certain functions on in The Global Langlands Correspondence for Function Fields over a Finite Field. The function field (over a finite field) version of the cuspidal automorphic forms we define here are actually obtained as linear combinations of translates of such functions hence why it is enough to study them. In this post, we will discuss automorphic forms in more detail, beginning with the version over the field of rational numbers before generalizing to more general global fields.
Defining modular forms as functions on 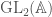
In a way, automorphic forms can also generalize modular forms (see also Modular Forms), and this will give us a way to connect the two theories. We shall take this route first and recast modular forms in a new language – instead of functions on the upper half-plane, we shall now look at them as functions on the group (here
denotes the adeles of
).
Let be a compact open subgroup of
whose elements all have determinants in
. Here
stands for the finite adeles, which are defined in the same way as the adeles, except we don’t include the infinite primes in the restricted product. We have that
where is the subgroup of
consisting of elements that have positive determinant. Now let us take the double quotient
. By the above expression for
as a product, we have
where is the subgroup of
given by projecting
into its archimedean component. Now suppose we are in the special case that
is given by
. Then it turns out that
is just
! Using appropriate choices of
, we can also obtain congruence subgroups such as
(see also Modular Forms).
The group acts on the upper half-plane by fractional linear transformations, i.e. if we have
, then
sends
in the upper half-plane to
. Let
.
Now given a modular form of weight
and level
, we may associate to it a function
on
as follows:
We can also go the other way, recovering from such a
:
for any such that
. Ultimately we want a function
on
, and we achieve this by setting
to just have the same value as
.
Translating properties of modular forms into properties of functions on 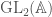
Invariance under 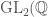 and
and 
Now we want to know what properties must have, so that we can determine which functions on
come from modular forms. We have just seen that we must have
.
The action of  and
and 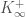
Let us now consider the action of the center of (which we denote by
) and the action of
, which is a maximal compact subgroup of
(and therefore we shall also denote it by
. The center
is composed of the matrices of the form
times the identity matrix, and it acts trivially on the upper half-plane. Therefore we will have
Now for the maximal compact subgroup . As previously mentioned, this is the group
, and may be expressed as matrices of the form
.
Then in the action of on the upper half-plane,
is the stabilizer of
. We will also have
This leads us to the second property our function must satisfy. First we consider
. For
, we must have
.
Note the appearance of the weight . Now when we extend this function
on
to a function
on
, we must replace
by its connected component
.
Holomorphicity and the action of the Lie algebra
Next we must translate the property that the modular form is holomorphic into a property of
. For this we shall introduce certain “raising” and “lowering” operators.
Let be the (real) Lie algebra of
. An element
acts on the space of smooth functions on
as follows:
We can extend this to an action of the complexified Lie algebra , defined to be
, by setting
We now look at two special elements of . They are
and
.
Let us now look at how these special elements act on the smooth functions on . We have
and
In other words, the action of raises the weight by
, while the action of
lowers the weight by
. Now it turns out that the condition that the function
on the upper half-plane is holomorphic is the same condition as the function
on
satisfying
!
Holomorphicity at the cusps
Now we have expressed the holomorphicity of our modular form as a condition on our function
on
. However not only do we want our modular forms to be holomorphic on the upper half-plane, we also want them to be “holomorphic at the cusps”, i.e. they do not go to infinity at the cusps. This is going to be accomplished by requiring the function
to be “slowly increasing” for all
. This means that for all
, we have
where and
are some positive constants and the norm on the right-hand side is given by, for
,
.
Summary of the properties
Let us summarize now the properties we want our function to have in order that it come from a modular form
:
- For all
, we have
.
- For all
, we have
.
- For all
, the function
is smooth.
- For all
we have
.
- The function
is invariant under
.
- We have
.
- The function given by
is slowly increasing.
Cuspidality
Now let us consider the case where is a cusp form. We want to translate the cuspidality condition to a condition on
, and we do this by noting that this means that the Fourier expansion of
has no constant term. Given that Fourier coefficients can be expressed using Fourier transforms, we make use of the measure theory on the adeles to express this cuspidality condition as
.
Automorphic forms
We have now defined modular forms as functions on , and enumerated some of their important properties. Modular forms, as functions on
, turn out to be merely be specific examples of more general functions on
that satisfy similar, but more relaxed, properties. These are the automorphic forms.
The first few properties are the same, for instance for all , we want
, and for all
, where
is a compact subgroup of
, we want
. We will also want the function given by
to be smooth for all
.
What we want to relax a little bit is the conditions on the actions of ,
, and the Lie algebra
, in that we want the space we get by having them act on some function
to be finite-dimensional. Instead of looking at the action of the Lie algebra
, it is often convenient to instead look at the action of its universal enveloping algebra
. The universal enveloping algebra is an honest to goodness associative algebra that contains the Lie algebra (and is in fact generated by its elements) such that the commutator of the universal enveloping algebra gives the Lie bracket of the Lie algebra. We shall denote the center of
by
. Now it turns out that
is generated by the Lie algebra of
and the Casimir operator
, defined to be
where is the element given by
. Therefore, the action of the center of the universal enveloping algebra encodes the action of
and the Lie algebra
at the same time.
Let us now define automorphic forms in general. Even though the focus on this post is on and over the rational numbers
, we can just give the most general definition of automorphic forms now, even for more general reductive groups and more general global fields. So let
be a reductive group and let
be a global field. The space of automorphic forms on
, denoted
, is the space of functions
satisfying the following properties:
- For all
, we have
.
- For all
,
a compact open subgroup of
, we have
.
- For all
, the function
is smooth.
- The function
is
-finite, i.e. the space
is finite dimensional.
- The function
is
-finite, i.e. the space
is finite dimensional.
- The function
is slowly increasing.
Here slowly increasing means that for all embeddings of the infinite part of
, we have
.
Furthermore, we say that the automorphic form is cuspidal if, for all parabolic subgroups
,
satisfies the following additional condition:
where is the unipotent radical (the unipotent part of the maximal connected normal solvable subgroup) of the parabolic subgroup
.
These cuspidal automorphic forms, which we denote by , form a subspace of the automorphic forms
.
Automorphic forms and representation theory
As stated earlier, automorphic forms give us a way of understanding the representation theory of where
is a reductive group. Let us now discuss these representation-theoretic aspects.
We will actually look at automorphic forms not as representations of , but as
-modules. This means they have actions of
,
, and
all satisfying certain compatibility conditions. A
-module is called admissible if any irreducible representation
shows up inside it with finite multiplicity, and irreducible if it has no proper subspaces fixed by
,
, and
. Recall from The Local Langlands Correspondence for General Linear Groups, irreducible admissible representations of
, where
is some local field, are precisely the kinds of representations that show up in the automorphic side of the local Langlands correspondence.
In fact the global and the local picture are related by Flath’s theorem, which says that, for an irreducible admissible -module
, we have the following factorization
into a restricted tensor product (explained in the next paragraph) of irreducible admissible representations of
, running over all places
of
. At the infinite place,
is an irreducible admissible
-module.
The restricted tensor product is a direct limit over of
where for
we have the inclusion
given by
, where
is a vector fixed by a certain maximal compact open subgroup (called hyperspecial)
of
(a representation of
containing such a fixed vector is called unramified).
We have that and
are
-modules. An automorphic representation of a reductive group
is an indecomposable
-module that is isomorphic to a subquotient of
. A cuspidal automorphic representation is an automorphic representation that is isomorphic to a subquotient of
. It is a property of the space of cuspidal automorphic forms that it is semisimple, i.e. it decomposes into a direct product of cuspidal automorphic representations (a property that is not necessarily shared by the bigger space of automorphic forms!).
An automorphic form generates such an automorphic representation, and a theorem of Harish-Chandra states that such a representation is admissible. In fact, automorphic representations are always admissible. Again recalling that irreducible admissible representations of make up the automorphic side of the local Langlands correspondence, we therefore expect that automorphic representations of
will make up the automorphic side of the global Langlands correspondence.
However, to state the original global Langlands correspondence in general is still quite complicated, as it involves an as of-yet hypothetical object called the Langlands group, which plays a somewhat analogous role as the Weil group in the local Langlands correspondence. Instead there are certain variants of it that are considered easier to approach, for instance by imposing conditions on the representations such as being “algebraic at infinity“. These variants of the global Langlands correspondence will hopefully be discussed in future posts.
References:
Automorphic form on Wikipedia
Topics in automorphic forms (notes by Chao Li from a course by Jack Thorne)
MSRI Summer School on Automorphic Forms and the Langlands Program by Kevin Buzzard
An Introduction to the Langlands Program by Daniel Bump, James W. Cogdell, Ehud de Shalit, Dennis Gaitsgory, Emmanuel Kowalski, and Stephen S. Kudla (edited by Joseph Bernstein and Stephen Gelbart)
Pingback: Completed Cohomology | Theories and Theorems
Pingback: The Theta Correspondence | Theories and Theorems