In The Global Langlands Correspondence for Function Fields over a Finite Field, we introduced the global Langlands correspondence for function fields over a finite field, and Vincent Lafforgue’s work on the automorphic to Galois direction of the correspondence. In this post we will discuss the work of Laurent Fargues and Peter Scholze which uses similar ideas but applies it to the local Langlands correspondence (and this time it works not only for “equal characteristic” cases like Laurent series fields 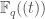 but also for “mixed characteristic” cases like finite extensions of
but also for “mixed characteristic” cases like finite extensions of 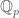 ). Note that instead of having complex coefficients like in The Local Langlands Correspondence for General Linear Groups, here we will use
). Note that instead of having complex coefficients like in The Local Langlands Correspondence for General Linear Groups, here we will use 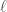 -adic coefficients.
-adic coefficients.
I. The Fargues-Fontaine Curve
Let us briefly discuss the idea of “geometrization” and what is meant by Fargues and Scholze making use of V. Lafforgue’s work. Recall that V. Lafforgue’s work concerns the global Langlands correspondence for function fields over a finite field  , which on one side concerns the space of cuspidal automorphic forms, which are certain functions on
, which on one side concerns the space of cuspidal automorphic forms, which are certain functions on 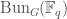 , which in turn parametrizes
, which in turn parametrizes  -bundles on some curve
-bundles on some curve  over
over  , and on the other side concerns representations (or more precisely L-parameters) of the etale fundamental group of
, and on the other side concerns representations (or more precisely L-parameters) of the etale fundamental group of  (which can also be phrased in terms of the Galois group of its function field).
(which can also be phrased in terms of the Galois group of its function field).
Perhaps the first question that comes to mind is, what is the analogue of the curve  in the case of the local Langlands correspondence when the field is not a function field (or more correctly a power series field, since it has to be local) over
in the case of the local Langlands correspondence when the field is not a function field (or more correctly a power series field, since it has to be local) over  , but some finite extension of
, but some finite extension of 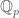 ? Let
? Let 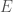 be this finite extension of
be this finite extension of 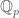 . Since the absolute Galois group of
. Since the absolute Galois group of 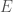 is also the etale fundamental group of
is also the etale fundamental group of 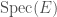 , perhaps we should take
, perhaps we should take 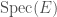 to be our analogue of
to be our analogue of  .
.
However, in the traditional formulation of the local Langlands correspondence, it is the Weil group that appears instead of the absolute Galois group itself. Considering the theory of the Weil group in Weil-Deligne Representations, this means that we will actually want 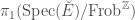 , where
, where 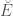 is the maximal unramified extension of
is the maximal unramified extension of 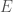 and
and 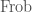 is the Frobenius, instead of
is the Frobenius, instead of 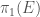 .
.
Now, we want to “relativize” this. For instance, in The Global Langlands Correspondence for Function Fields over a Finite Field, we considered 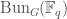 , which parametrizes
, which parametrizes  -bundles on the curve
-bundles on the curve  over
over  . But we may also want to consider say
. But we may also want to consider say 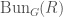 , where
, where  is some
is some  -algebra; this would parametrize
-algebra; this would parametrize  -bundles on
-bundles on  instead. In fact, we need this “relativization” to properly define
instead. In fact, we need this “relativization” to properly define 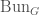 as a stack (see also Algebraic Spaces and Stacks).
as a stack (see also Algebraic Spaces and Stacks).
The problem with transporting this to the case of  a finite extension of
a finite extension of  is that we do not have an “base” like
is that we do not have an “base” like  was for the function field case (unless perhaps if we have something like an appropriate version of the titular object in The Field with One Element, which is at the moment unavailable). The solution to this is provided by the theory of adic spaces and perfectoid spaces (see also Adic Spaces and Perfectoid Spaces).
was for the function field case (unless perhaps if we have something like an appropriate version of the titular object in The Field with One Element, which is at the moment unavailable). The solution to this is provided by the theory of adic spaces and perfectoid spaces (see also Adic Spaces and Perfectoid Spaces).
For motivation, let us consider first the case where our field is 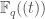 . Let
. Let 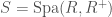 be a perfectoid space over
be a perfectoid space over  with pseudouniformizer
with pseudouniformizer  . Consider the product
. Consider the product 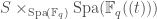 . We may look at this as the punctured open unit disc over
. We may look at this as the punctured open unit disc over  . It sits inside
. It sits inside ![\mathrm{Spa}(R^{+})\times_{\mathrm{Spa}(\mathbb{F}_{q})}\mathrm{Spa}(\mathbb{F}_{q}[[t]])](https://s0.wp.com/latex.php?latex=%5Cmathrm%7BSpa%7D%28R%5E%7B%2B%7D%29%5Ctimes_%7B%5Cmathrm%7BSpa%7D%28%5Cmathbb%7BF%7D_%7Bq%7D%29%7D%5Cmathrm%7BSpa%7D%28%5Cmathbb%7BF%7D_%7Bq%7D%5B%5Bt%5D%5D%29&bg=ffffff&fg=444444&s=0&c=20201002) as the locus where the pseudo-uniformizer
as the locus where the pseudo-uniformizer  of
of  and the uniformizer
and the uniformizer  of
of ![\mathbb{F}_{q}[[t]]](https://s0.wp.com/latex.php?latex=%5Cmathbb%7BF%7D_%7Bq%7D%5B%5Bt%5D%5D&bg=ffffff&fg=444444&s=0&c=20201002) is invertible (or “nonzero”).
is invertible (or “nonzero”).
In the case where our field is 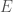 , a finite extension of
, a finite extension of 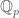 , as mentioned earlier we have no “base” like
, as mentioned earlier we have no “base” like  was for
was for 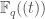 . So we cannot form the fiber products analogous to
. So we cannot form the fiber products analogous to 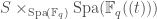 or
or ![\mathrm{Spa}(R^{+})\times_{\mathrm{Spa}(\mathbb{F}_{q})}\mathrm{Spa}(\mathbb{F}_{q}[[t]])](https://s0.wp.com/latex.php?latex=%5Cmathrm%7BSpa%7D%28R%5E%7B%2B%7D%29%5Ctimes_%7B%5Cmathrm%7BSpa%7D%28%5Cmathbb%7BF%7D_%7Bq%7D%29%7D%5Cmathrm%7BSpa%7D%28%5Cmathbb%7BF%7D_%7Bq%7D%5B%5Bt%5D%5D%29&bg=ffffff&fg=444444&s=0&c=20201002) . However, notice that
. However, notice that
![\displaystyle \mathrm{Spa}(R^{+})\times_{\mathrm{Spa}(\mathbb{F}_{q})}\mathrm{Spa}(\mathbb{F}_{q}[[t]])\cong \mathrm{Spa}(R^{+}[[t]])](https://s0.wp.com/latex.php?latex=%5Cdisplaystyle+%5Cmathrm%7BSpa%7D%28R%5E%7B%2B%7D%29%5Ctimes_%7B%5Cmathrm%7BSpa%7D%28%5Cmathbb%7BF%7D_%7Bq%7D%29%7D%5Cmathrm%7BSpa%7D%28%5Cmathbb%7BF%7D_%7Bq%7D%5B%5Bt%5D%5D%29%5Ccong+%5Cmathrm%7BSpa%7D%28R%5E%7B%2B%7D%5B%5Bt%5D%5D%29&bg=ffffff&fg=444444&s=0&c=20201002) .
.
This has an analogue in the mixed-characteristic, given by the theory of Witt vectors (compare, for instance ![\mathbb{F}_{p}[[t]]](https://s0.wp.com/latex.php?latex=%5Cmathbb%7BF%7D_%7Bp%7D%5B%5Bt%5D%5D&bg=ffffff&fg=444444&s=0&c=20201002) and its “mixed-characteristic analogue”
and its “mixed-characteristic analogue”  )! If
)! If  is the residue field of
is the residue field of 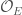 , we define the ramified Witt vectors
, we define the ramified Witt vectors 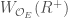 to be
to be 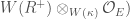 . This is the analogue of
. This is the analogue of ![\mathrm{Spa}(R^{+})\times_{\mathrm{Spa}(\mathbb{F}_{q})}\mathrm{Spa}(\mathbb{F}_{q}[[t]])](https://s0.wp.com/latex.php?latex=%5Cmathrm%7BSpa%7D%28R%5E%7B%2B%7D%29%5Ctimes_%7B%5Cmathrm%7BSpa%7D%28%5Cmathbb%7BF%7D_%7Bq%7D%29%7D%5Cmathrm%7BSpa%7D%28%5Cmathbb%7BF%7D_%7Bq%7D%5B%5Bt%5D%5D%29&bg=ffffff&fg=444444&s=0&c=20201002) . Now all we have to do to find the analogue of
. Now all we have to do to find the analogue of 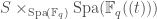 that we are looking for is to define it as the locus in
that we are looking for is to define it as the locus in 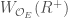 where both the uniformizer
where both the uniformizer  of
of  and the uniformizer
and the uniformizer  of
of 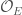 are invertible!
are invertible!
We denote this locus by 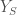 . But recall again our discussion earlier, that due to the local Langlands correspondence being phrased in terms of the Weil group, we have to quotient out by the powers of Frobenius. Therefore we define the Fargues-Fontaine curve
. But recall again our discussion earlier, that due to the local Langlands correspondence being phrased in terms of the Weil group, we have to quotient out by the powers of Frobenius. Therefore we define the Fargues-Fontaine curve 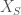 to be
to be 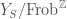 .
.
Aside from our purpose of geometrizing the local Langlands correspondence, the Fargues-Fontaine curve 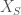 is in itself a very interesting mathematical object. For instance, when
is in itself a very interesting mathematical object. For instance, when  is a complete algebraically closed nonarchimedean field over
is a complete algebraically closed nonarchimedean field over  , the classical points of
, the classical points of 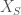 (i.e. maximal ideals of the rings
(i.e. maximal ideals of the rings 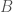 such that
such that 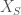 is locally
is locally 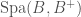 ) correspond to untilts of
) correspond to untilts of  (modulo the action of Frobenius)!
(modulo the action of Frobenius)!
There is also a similar notion for more general  . To explain this we need the concept of diamonds, which will also be very important for the rest of the post. A diamond is a pro-etale sheaf on the category of perfectoid spaces over
. To explain this we need the concept of diamonds, which will also be very important for the rest of the post. A diamond is a pro-etale sheaf on the category of perfectoid spaces over 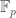 , which is the quotient of some perfectoid space
, which is the quotient of some perfectoid space  over
over 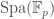 by a pro-etale equivalence relation
by a pro-etale equivalence relation 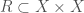 (we also say that the diamond is a coequalizer). An example of a diamond is given by
(we also say that the diamond is a coequalizer). An example of a diamond is given by  . Note that
. Note that 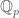 is not perfectoid, but is the quotient of a perfectoid field we denoted
is not perfectoid, but is the quotient of a perfectoid field we denoted  in Adic Spaces and Perfectoid Spaces by the action of
in Adic Spaces and Perfectoid Spaces by the action of 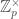 . Now we can take the tilt
. Now we can take the tilt  and quotient out by
and quotient out by 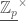 (the underline notation will be explained later – for now we think of this as making the group
(the underline notation will be explained later – for now we think of this as making the group 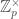 into a perfectoid space) – this is the diamond
into a perfectoid space) – this is the diamond  . More generally, if
. More generally, if  is an adic space over
is an adic space over  satisfying certain conditions (“analytic”), we can define the diamond
satisfying certain conditions (“analytic”), we can define the diamond 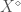 to be such that
to be such that 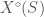 , for
, for  a perfectoid space over
a perfectoid space over 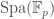 , is the set of isomorphism classes of pairs
, is the set of isomorphism classes of pairs 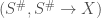 ,
, 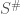 being the untilt of
being the untilt of  . If
. If  , we also use
, we also use 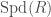 to denote
to denote 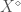 . Note that if
. Note that if  is already perfectoid,
is already perfectoid, 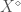 is just the same thing as the tilt
is just the same thing as the tilt 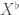 .
.
Now recall that 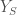 was defined to be the locus in
was defined to be the locus in  where the uniformizer
where the uniformizer  of
of  and the uniformizer
and the uniformizer  of
of 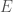 were invertible. We actually have that
were invertible. We actually have that 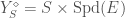 , and, for the Fargues-Fontaine curve
, and, for the Fargues-Fontaine curve 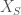 , we have that
, we have that 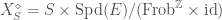 .
.
Our generalization of the statement that the points of 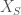 parametrize untilts of
parametrize untilts of  is now as follows. There exists a three-way bijection between sections of the map
is now as follows. There exists a three-way bijection between sections of the map 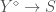 , maps
, maps 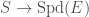 , and untilts
, and untilts 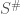 over
over 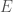 of
of  . Given such an untilt
. Given such an untilt 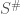 , this defines a closed Cartier divisor on
, this defines a closed Cartier divisor on 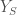 , which in turn gives rise to a closed Cartier divisor on
, which in turn gives rise to a closed Cartier divisor on 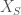 . By the bijection mentioned earlier, these closed Cartier divisors on
. By the bijection mentioned earlier, these closed Cartier divisors on  will be parametrized by maps
will be parametrized by maps 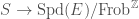 .
.
The closed Cartier divisors that arise in this way will be referred to as closed Cartier divisors of degree 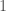 . We have seen that they are parametrized by the following moduli space we denote by
. We have seen that they are parametrized by the following moduli space we denote by 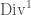 (this will also become important later on):
(this will also become important later on):
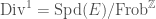
Now that we have discussed the Fargues-Fontaine curve 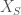 and some of its properties, we can define
and some of its properties, we can define 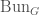 as the stack that assigns to any perfectoid space
as the stack that assigns to any perfectoid space  over
over  the groupoid of
the groupoid of  -bundles on
-bundles on 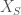 .
.
When 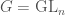 , our
, our  -bundles are just vector bundles. In this case we shall also denote
-bundles are just vector bundles. In this case we shall also denote 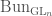 by
by 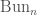 .
.
II. Vector Bundles on the Fargues-Fontaine Curve
Let us now try to understand a little bit more about vector bundles on the Fargues-Fontaine curve. They turn out to be related to another important thing in arithmetic geometry – isocrystals – and this will allow us to classify them completely.
Let 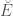 be the completion of the maximal unramified extension of
be the completion of the maximal unramified extension of 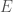 . Letting
. Letting  denote the residue field of
denote the residue field of 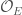 ,
, 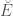 may also be expressed as the fraction field of
may also be expressed as the fraction field of 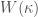 . It is equipped with a Frobenius lift
. It is equipped with a Frobenius lift 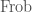 . An isocrystal
. An isocrystal  over
over 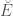 is defined to be a vector space over
is defined to be a vector space over 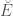 equipped with a
equipped with a 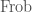 -semilinear automorphism.
-semilinear automorphism.
Given an isocrystal  over
over 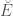 , we can obtain a vector bundle
, we can obtain a vector bundle 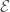 on the Fargues-Fontaine curve
on the Fargues-Fontaine curve 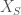 by defining
by defining 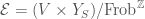 . It turns out all the vector bundles over
. It turns out all the vector bundles over 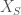 can be obtained in this way!
can be obtained in this way!
Now the advantage of relating vector bundles on the Fargues-Fontaine curve to isocrystals is that isocrystals are completely classified via the Dieudonne-Manin classification. This says that the category of isocrystals over 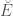 is semi-simple (so every object is a direct sum of the simple objects), and the form of the simple objects are completely determined by two integers which are coprime, the rank (i.e. the dimension as an
is semi-simple (so every object is a direct sum of the simple objects), and the form of the simple objects are completely determined by two integers which are coprime, the rank (i.e. the dimension as an  -vector space)
-vector space) 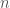 which must be positive, and the degree (which determines the form of the
which must be positive, and the degree (which determines the form of the 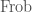 -semilinear automorphism)
-semilinear automorphism) 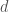 . Since these two integers are coprime and one is positive, there is really only one number that completely determines a simple
. Since these two integers are coprime and one is positive, there is really only one number that completely determines a simple 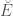 -isocrystal – its slope, defined to be the rational number
-isocrystal – its slope, defined to be the rational number 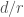 . Therefore we shall also often denote a simple
. Therefore we shall also often denote a simple 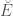 -isocrystal as
-isocrystal as 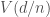 . Since isocrystals over
. Since isocrystals over 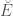 and vector bundles on the Fargues-Fontaine curve
and vector bundles on the Fargues-Fontaine curve 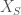 are in bijection, if we have a simple
are in bijection, if we have a simple 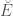 -isocrystal
-isocrystal 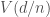 we shall denote the corresponding vector bundle by
we shall denote the corresponding vector bundle by 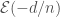 . More generally, an isocrystal is a direct sum of simple isocrystals and they can have different slopes. If an isocrystal only has one slope, we say that it is semistable (or basic). We use the same terminology for the corresponding vector bundle.
. More generally, an isocrystal is a direct sum of simple isocrystals and they can have different slopes. If an isocrystal only has one slope, we say that it is semistable (or basic). We use the same terminology for the corresponding vector bundle.
More generally, for more general reductive groups  , we have a notion of
, we have a notion of  -isocrystals; this can also be thought of functors from the category of representations of
-isocrystals; this can also be thought of functors from the category of representations of  over
over 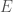 to the category of isocrystals over
to the category of isocrystals over 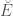 . These are in correspondence with
. These are in correspondence with  -bundles over the Fargues-Fontaine curve. There is also a notion of semistable or basic for
-bundles over the Fargues-Fontaine curve. There is also a notion of semistable or basic for  -isocrystals, although its definition involves the Newton invariant (one of two important invariants of a
-isocrystals, although its definition involves the Newton invariant (one of two important invariants of a  -isocrystal, the other being the Kottwitz invariant).
-isocrystal, the other being the Kottwitz invariant).
The set of  -isocrystals is denoted
-isocrystals is denoted 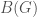 and is also called the Kottwitz set. This set is in fact also in bijection with the equivalence classes in
and is also called the Kottwitz set. This set is in fact also in bijection with the equivalence classes in 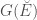 under “Frobenius-twisted conjugacy”, i.e. the equivalence relation
under “Frobenius-twisted conjugacy”, i.e. the equivalence relation 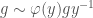 . Given an element
. Given an element 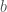 of
of 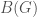 , we can define the algebraic group
, we can define the algebraic group 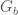 to be such that the elements of
to be such that the elements of 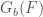 are the elements
are the elements 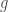 of
of 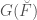 satisfying the condition
satisfying the condition 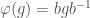 . If
. If  , then
, then 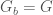 .
.
The groups 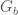 are inner forms of
are inner forms of  (see also Reductive Groups Part II: Over More General Fields). More precisely, the
(see also Reductive Groups Part II: Over More General Fields). More precisely, the 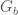 are the extended pure inner forms of
are the extended pure inner forms of  , which are all the inner forms of
, which are all the inner forms of  if the center of
if the center of  is connected. Groups which are inner forms of each other are in some way closely related under the local Langlands correspondence – for instance, they have the same Langlands dual group. It has been proposed that these inner forms should really be studied “together” in some way, and we shall see that the use of
is connected. Groups which are inner forms of each other are in some way closely related under the local Langlands correspondence – for instance, they have the same Langlands dual group. It has been proposed that these inner forms should really be studied “together” in some way, and we shall see that the use of 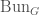 to formulate the local Langlands correspondence provides a realization of this approach.
to formulate the local Langlands correspondence provides a realization of this approach.
Let us mention one more important part of arithmetic geometry that vector bundles on the Fargues-Fontaine curve are related to, namely p-divisible groups. A p-divisible group (also known as a Barsotti-Tate group)  is an direct limit of group schemes
is an direct limit of group schemes
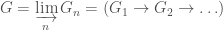
such that  is a finite flat commutative group scheme which is
is a finite flat commutative group scheme which is 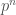 -torsion of order
-torsion of order 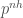 and such that the inclusion
and such that the inclusion 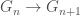 induces an isomorphism of
induces an isomorphism of  with
with ![G_{n+1}[p^{n}]](https://s0.wp.com/latex.php?latex=G_%7Bn%2B1%7D%5Bp%5E%7Bn%7D%5D&bg=ffffff&fg=444444&s=0&c=20201002) (the kernel of the multiplication by
(the kernel of the multiplication by 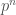 map in
map in  ). The number
). The number 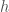 is called the height of the p-divisible group.
is called the height of the p-divisible group.
An example of a p-divisible group is given by 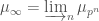 . This is a p-divisible group of height
. This is a p-divisible group of height 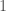 . Given an abelian variety of dimension
. Given an abelian variety of dimension 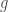 , we can also form a p-divisible group of height
, we can also form a p-divisible group of height 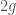 by taking the direct limit of its
by taking the direct limit of its  -torsion.
-torsion.
We can also obtain p-divisible groups from formal group laws (see also The Lubin-Tate Formal Group Law) by taking the direct limit of its 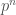 -torsion. In this case we can then define the dimension of such a p-divisible group to be the dimension of the formal group law it was obtained from. More generally, for any p-divisible group over a complete Noetherian local ring of residue characteristic
-torsion. In this case we can then define the dimension of such a p-divisible group to be the dimension of the formal group law it was obtained from. More generally, for any p-divisible group over a complete Noetherian local ring of residue characteristic  , the connected component of its identity always comes from a formal group law in this way, and so we can define the dimension of the p-divisible group to be the dimension of this connected component.
, the connected component of its identity always comes from a formal group law in this way, and so we can define the dimension of the p-divisible group to be the dimension of this connected component.
Now it turns out p-divisible groups can also be classified by a single number, the slope, defined to be the dimension divided by the height. If the terminology appears suggestive of the classification of isocrystals and vector bundles on the Fargues-Fontaine curve, that’s because it is! Isocrystals (and therefore vector bundles on the Fargues-Fontaine curve) and p-divisible groups are in bijection with each other, at least in the case where the slope is between 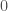 and
and 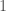 . This is quite important because the cohomology of deformation spaces of p-divisible groups (such as that obtained from the Lubin-Tate group law) have been used to prove the local Langlands correspondence before the work of Fargues and Scholze! We will be revisiting this later.
. This is quite important because the cohomology of deformation spaces of p-divisible groups (such as that obtained from the Lubin-Tate group law) have been used to prove the local Langlands correspondence before the work of Fargues and Scholze! We will be revisiting this later.
III. The Geometry of 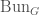
Let us now discuss more about the geometry of 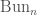 . It happens that
. It happens that 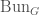 is a small v-sheaf. A v-sheaf is a sheaf on the category of perfectoid spaces over
is a small v-sheaf. A v-sheaf is a sheaf on the category of perfectoid spaces over  equipped with the v-topology, where the covers of
equipped with the v-topology, where the covers of  are any maps
are any maps 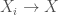 such that for any quasicompact
such that for any quasicompact 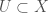 there are finitely many
there are finitely many 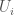 which cover
which cover 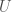 . A v-sheaf is small if it admits a surjective map from a perfectoid space. In particular being a small v-sheaf implies that
. A v-sheaf is small if it admits a surjective map from a perfectoid space. In particular being a small v-sheaf implies that 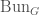 has an underlying topological space
has an underlying topological space 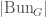 . The points of this topological space are going to be in bijection with the elements of the Kottwitz set
. The points of this topological space are going to be in bijection with the elements of the Kottwitz set 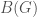 .
.
If  is a locally profinite topological group, we define
is a locally profinite topological group, we define  to be the functor from perfectoid spaces over
to be the functor from perfectoid spaces over  which sends a perfectoid space
which sends a perfectoid space  over
over  to the set
to the set 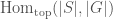 . We let
. We let ![[\ast/\underline{G}]](https://s0.wp.com/latex.php?latex=%5B%5Cast%2F%5Cunderline%7BG%7D%5D&bg=ffffff&fg=444444&s=0&c=20201002) be the classifying stack of
be the classifying stack of  -bundles; this means that we can obtain any
-bundles; this means that we can obtain any  -bundle on any perfectoid space
-bundle on any perfectoid space  over
over  by pulling back a universal
by pulling back a universal  -bundle on
-bundle on ![[\ast/\underline{G}]](https://s0.wp.com/latex.php?latex=%5B%5Cast%2F%5Cunderline%7BG%7D%5D&bg=ffffff&fg=444444&s=0&c=20201002) .
.
We write 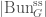 for the locus in
for the locus in 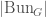 corresponding to the
corresponding to the  -isocrystals that are semistable. We let
-isocrystals that are semistable. We let  the substack of
the substack of 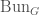 whose underlying topological space is
whose underlying topological space is 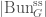 . It turns out that we have a decomposition
. It turns out that we have a decomposition
![\displaystyle \mathrm{Bun}_{G}^{\mathrm{ss}}\cong\coprod_{b\in B(G)_{\mathrm{basic}}}[\ast/\underline{G_{b}(E)}]](https://s0.wp.com/latex.php?latex=%5Cdisplaystyle+%5Cmathrm%7BBun%7D_%7BG%7D%5E%7B%5Cmathrm%7Bss%7D%7D%5Ccong%5Ccoprod_%7Bb%5Cin+B%28G%29_%7B%5Cmathrm%7Bbasic%7D%7D%7D%5B%5Cast%2F%5Cunderline%7BG_%7Bb%7D%28E%29%7D%5D&bg=ffffff&fg=444444&s=0&c=20201002)
More generally, even is 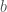 is not basic, we have an inclusion
is not basic, we have an inclusion
![\displaystyle j:[\ast/\underline{G_{b}(E)}]\hookrightarrow \mathrm{Bun}_{G}](https://s0.wp.com/latex.php?latex=%5Cdisplaystyle+j%3A%5B%5Cast%2F%5Cunderline%7BG_%7Bb%7D%28E%29%7D%5D%5Chookrightarrow+%5Cmathrm%7BBun%7D_%7BG%7D&bg=ffffff&fg=444444&s=0&c=20201002)
Let us now look at some more of the properties of 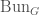 . In particular,
. In particular, 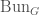 satisfies the conditions for an analogue of an Artin stack (see also Algebraic Spaces and Stacks) but with locally spatial diamonds instead of algebraic spaces and schemes.
satisfies the conditions for an analogue of an Artin stack (see also Algebraic Spaces and Stacks) but with locally spatial diamonds instead of algebraic spaces and schemes.
A diamond  is called a spatial diamond if it is quasicompact quasiseparated, and its underlying topological space
is called a spatial diamond if it is quasicompact quasiseparated, and its underlying topological space  is generated by
is generated by  , where
, where 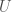 runs over all sub-diamonds of
runs over all sub-diamonds of  which are quasicompact. A diamond is called a locally spatial diamond if it admits an open cover by spatial diamonds.
which are quasicompact. A diamond is called a locally spatial diamond if it admits an open cover by spatial diamonds.
Now we recall from Algebraic Spaces and Stacks that to be an Artin stack, a stack must have a diagonal that is representable in algebraic spaces, and it has charts which are representable by schemes. It turns out 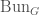 satisfies analogous properties – its diagonal is representable in locally spatial diamonds, and it has charts which are representable by locally spatial diamonds.
satisfies analogous properties – its diagonal is representable in locally spatial diamonds, and it has charts which are representable by locally spatial diamonds.
We can now define a derived category (see also Perverse Sheaves and the Geometric Satake Equivalence) of sheaves on the v-site of 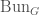 with coefficients in some
with coefficients in some 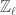 -algebra
-algebra  . If
. If  is torsion (e.g.
is torsion (e.g.  or
or  ), this can be the category
), this can be the category 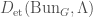 , which is the subcategory of
, which is the subcategory of 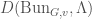 whose pullback to any strictly disconnected perfectoid space
whose pullback to any strictly disconnected perfectoid space  lands in
lands in 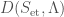 (here the subscripts
(here the subscripts  and
and  denote the v-site and the etale site respectively). If
denote the v-site and the etale site respectively). If  is not torsion (e.g.
is not torsion (e.g. 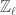 or
or 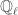 ) one needs the notion of solid modules (which was further developed in the work of Clausen and Scholze on condensed mathematics) to construct the right derived category.
) one needs the notion of solid modules (which was further developed in the work of Clausen and Scholze on condensed mathematics) to construct the right derived category.
If  is a spatial diamond and
is a spatial diamond and 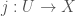 is a pro-etale map expressible as a limit of etale maps
is a pro-etale map expressible as a limit of etale maps 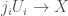 , we can construct the sheaf
, we can construct the sheaf ![\widehat{\mathbb{Z}}[U]](https://s0.wp.com/latex.php?latex=%5Cwidehat%7B%5Cmathbb%7BZ%7D%7D%5BU%5D&bg=ffffff&fg=444444&s=0&c=20201002) as the limit
as the limit  . We say that a sheaf
. We say that a sheaf  on
on  is solid if
is solid if  is isomorphic to
is isomorphic to ![\mathrm{Hom}(\widehat{\mathbb{Z}}[U],\mathcal{F})](https://s0.wp.com/latex.php?latex=%5Cmathrm%7BHom%7D%28%5Cwidehat%7B%5Cmathbb%7BZ%7D%7D%5BU%5D%2C%5Cmathcal%7BF%7D%29&bg=ffffff&fg=444444&s=0&c=20201002) . We can extend this to small v-stacks – if
. We can extend this to small v-stacks – if  is a small v-stack and
is a small v-stack and 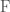 is a v-sheaf on
is a v-sheaf on  , we say that
, we say that  is solid if for every map from a spatial diamond
is solid if for every map from a spatial diamond  to
to  the pullback of
the pullback of  to
to  coincides with the pullback of a solid sheaf from the quasi-pro-etale site of
coincides with the pullback of a solid sheaf from the quasi-pro-etale site of  . We denote by
. We denote by 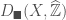 the subcategory of
the subcategory of 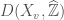 whose objects have cohomology sheaves which are solid. Now if we have a solid
whose objects have cohomology sheaves which are solid. Now if we have a solid 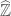 -algebra
-algebra  , we can consider
, we can consider 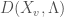 inside
inside 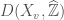 , and we denote by
, and we denote by 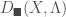 the subcategory of objects of
the subcategory of objects of 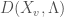 whose image in
whose image in 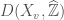 is solid.
is solid.
This category 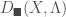 is still too big for our purposes. Therefore we cut out a subcategory
is still too big for our purposes. Therefore we cut out a subcategory 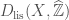 as follows. If we have a map of v-stacks
as follows. If we have a map of v-stacks 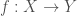 , we have a pullback map
, we have a pullback map 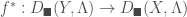 . This pullback map has a left-adjoint
. This pullback map has a left-adjoint 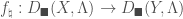 . We define
. We define 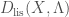 to be the smallest triangulated subcategory stable under direct sums that contain
to be the smallest triangulated subcategory stable under direct sums that contain 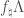 , for all
, for all 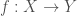 which are separated, representable by locally spatial diamonds, and
which are separated, representable by locally spatial diamonds, and 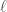 -cohomologically smooth. If
-cohomologically smooth. If  is torsion, then
is torsion, then 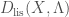 coincides with
coincides with 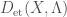 .
.
Let  be the derived category of smooth representations of the group
be the derived category of smooth representations of the group  over
over  . We have
. We have

Now taking the pushforward of this derived category of sheaves through the inclusion 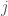 , and using the isomorphism above, we get
, and using the isomorphism above, we get
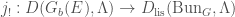
Now we can see that this derived category 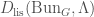 of sheaves on
of sheaves on 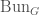 encodes the representation theory of
encodes the representation theory of  , which is one side of the local Langlands correspondence, but more than that, it encodes the representation theory of all the extended pure inner forms of
, which is one side of the local Langlands correspondence, but more than that, it encodes the representation theory of all the extended pure inner forms of  altogether.
altogether.
The properties of 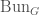 mentioned earlier, in particular its charts which are representable by locally spatial diamonds, allow us to define properties of objects in
mentioned earlier, in particular its charts which are representable by locally spatial diamonds, allow us to define properties of objects in 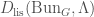 which translate into properties of interest in
which translate into properties of interest in  . For example, we have a notion of
. For example, we have a notion of 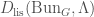 being compactly generated, and this translates into a notion of compactness for
being compactly generated, and this translates into a notion of compactness for  . We also have a notion of Bernstein-Zelevinsky duality for
. We also have a notion of Bernstein-Zelevinsky duality for 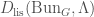 , which translates into Bernstein-Zelevinsky duality for
, which translates into Bernstein-Zelevinsky duality for  , and finally, we have a notion of universal local acyclicity in
, and finally, we have a notion of universal local acyclicity in 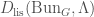 , which translates into being admissible for
, which translates into being admissible for  .
.
IV. The Hecke Correspondence and Excursion Operators
Now let us look at how the strategy in The Global Langlands Correspondence for Function Fields over a Finite Field works for our setup. We will be working in the “geometric” setting (i.e. sheaves or complexes of sheaves instead of functions) mentioned at the end of that post, so there will be some differences from the work of Lafforgue that we discussed there, although the motivations and main ideas (e.g. excursion operators) will be somewhat similar.
Just like in The Global Langlands Correspondence for Function Fields over a Finite Field, we will have a Hecke stack  that parametrizes modifications of
that parametrizes modifications of  -bundles over the Fargues-Fontaine curve. This means that
-bundles over the Fargues-Fontaine curve. This means that 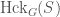 is the groupoid of triples
is the groupoid of triples  where
where 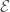 and
and  are
are  -bundles over
-bundles over 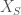 and
and  is an isomorphism of vector bundles meromorphic on some degree
is an isomorphism of vector bundles meromorphic on some degree 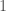 Cartier divisor
Cartier divisor 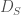 on
on 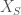 (which is part of the data of the modification). Note that we have maps
(which is part of the data of the modification). Note that we have maps  and
and 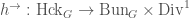 which sends the triple
which sends the triple 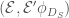 to
to 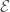 and
and 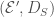 respectively.
respectively.
Now we need to bound the relative position of the modification. Recall that this is encoded via (conjugacy classes of) cocharacters 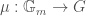 . The way this is done in this case is via the local Hecke stack
. The way this is done in this case is via the local Hecke stack  , which parametrizes modifications of
, which parametrizes modifications of  -bundles on the completion of
-bundles on the completion of 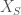 along
along 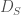 (compare the moduli stacks denoted
(compare the moduli stacks denoted 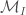 inThe Global Langlands Correspondence for Function Fields over a Finite Field). The local Hecke stack admits a stratification into Schubert cells labeled by conjugacy classes of cocharacters
inThe Global Langlands Correspondence for Function Fields over a Finite Field). The local Hecke stack admits a stratification into Schubert cells labeled by conjugacy classes of cocharacters 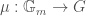 . We can now pull back a Schubert cell
. We can now pull back a Schubert cell 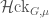 to the global Hecke stack
to the global Hecke stack  to get a substack
to get a substack 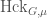 with maps
with maps 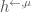 and
and  , and define a Hecke operator as
, and define a Hecke operator as

More generally, to consider compositions of Hecke operators we need to consider modifications at multiple points. For this we will need the geometric Satake equivalence.
Let  be an affinoid perfectoid space over
be an affinoid perfectoid space over  . For each
. For each  in some indexing set
in some indexing set 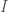 , we let
, we let  be a Cartier divisor on
be a Cartier divisor on 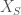 . Let
. Let 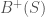 be the completion of
be the completion of 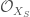 along the union of the
along the union of the  , and let
, and let  be the localization of
be the localization of 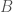 obtained by inverting the
obtained by inverting the  . For our reductive group
. For our reductive group  , we define the positive loop group
, we define the positive loop group 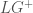 to be the functor which sends an affinoid perfectoid space
to be the functor which sends an affinoid perfectoid space  to
to  , and we define the loop group
, and we define the loop group  to be the functor which sends
to be the functor which sends  to
to 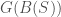 .
.
We define the Beilinson-Drinfeld Grassmannian 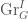 to be the quotient
to be the quotient  . We further define the local Hecke stack
. We further define the local Hecke stack 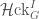 to be the quotient
to be the quotient 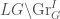 .
.
The geometric Satake equivalence tells us that the category 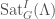 of perverse sheaves on
of perverse sheaves on 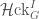 satisfying certain conditions (quasicompact over
satisfying certain conditions (quasicompact over  , flat over
, flat over  , universally locally acyclic) is equivalent to the category of representations of
, universally locally acyclic) is equivalent to the category of representations of 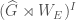 on finite projective
on finite projective  -modules.
-modules.
Let  be such a representation of representations of
be such a representation of representations of 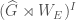 . Let
. Let 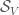 be the corresponding object of
be the corresponding object of 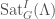 . The global Hecke stack
. The global Hecke stack 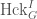 has a map
has a map  to the local Hecke stack
to the local Hecke stack 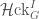 . It also has maps
. It also has maps 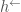 to
to 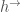 to
to 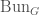 and
and 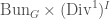 respectively. We can now define the Hecke operator
respectively. We can now define the Hecke operator 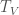 as follows:
as follows:
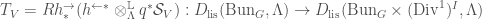
Once we have the Hecke operators, we can then consider excursion operators and apply the strategy of Lafforgue discussed in The Global Langlands Correspondence for Function Fields over a Finite Field. We set  to be
to be 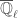 . Let
. Let 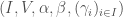 be an excursion datum, i.e.
be an excursion datum, i.e. 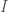 is a finite set,
is a finite set,  is a representation of
is a representation of 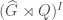 ,
,  ,
, 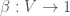 , and
, and  for all
for all 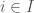 . An excursion operator is the following composition:
. An excursion operator is the following composition:

Now this composition turns out to be the same as multiplication by the scalar determined by the following composition:

And the 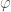 that appears here is precisely the L-parameter that we are looking for. This therefore gives us the “automorphic to Galois” direction of the local Langlands correspondence.
that appears here is precisely the L-parameter that we are looking for. This therefore gives us the “automorphic to Galois” direction of the local Langlands correspondence.
V. Relation to Local Class Field Theory
It is interesting to look at how this all works in the case  , i.e. local class field theory. There is historical precedent for this in the work of Pierre Deligne for what we might now call the
, i.e. local class field theory. There is historical precedent for this in the work of Pierre Deligne for what we might now call the  case of the (geometric) global Langlands correspondence for function fields over a finite field, but which might also be called geometric class field theory.
case of the (geometric) global Langlands correspondence for function fields over a finite field, but which might also be called geometric class field theory.
Let us go back to the setting in The Global Langlands Correspondence for Function Fields over a Finite Field, where we are working over a function field of some curve  over the finite field
over the finite field  . Since we are considering
. Since we are considering  , our
, our 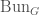 in this case will be the Picard group
in this case will be the Picard group  , which parametrizes line bundles on
, which parametrizes line bundles on  . The statement of the geometric Langlands correspondence in this case is that there is an equivalence of character sheaves on
. The statement of the geometric Langlands correspondence in this case is that there is an equivalence of character sheaves on  (see the discussion of Grothendieck’s sheaves to functions dictionary at the end of The Global Langlands Correspondence for Function Fields over a Finite Field) and
(see the discussion of Grothendieck’s sheaves to functions dictionary at the end of The Global Langlands Correspondence for Function Fields over a Finite Field) and 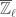 -local systems of rank
-local systems of rank 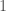 on
on  (these are the same as one-dimensional representations of
(these are the same as one-dimensional representations of 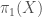 ).
).
We have an Abel-Jacobi map 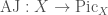 , sending a point
, sending a point  of
of  to the corresponding divisor
to the corresponding divisor  in
in  . More generally we can define
. More generally we can define 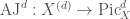 , where
, where 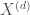 is the quotient of
is the quotient of 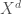 by the symmetric group on its factors, and
by the symmetric group on its factors, and 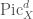 is the degree
is the degree 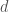 part of
part of  .
.
Now suppose we have a rank 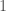
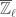 -local system on
-local system on  , which we shall denote by
, which we shall denote by  . We can form a local system
. We can form a local system  on
on 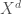 . We can push this forward to
. We can push this forward to 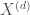 and get a sheaf
and get a sheaf 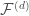 on
on 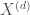 . What we hope for is that this sheaf
. What we hope for is that this sheaf 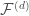 is the pullback of the character sheaf on
is the pullback of the character sheaf on 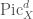 that we are looking for via
that we are looking for via 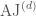 . This is in fact what happens, and what makes this possible is that the fibers of
. This is in fact what happens, and what makes this possible is that the fibers of 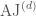 are simply connected for
are simply connected for 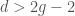 , by the Riemann-Roch theorem. So for this
, by the Riemann-Roch theorem. So for this 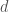 , by taking fundamental groups of the fiber sequence, we have that
, by taking fundamental groups of the fiber sequence, we have that 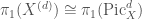 . So representations of
. So representations of 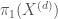 give rise to representations of
give rise to representations of 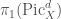 , and since representations of the fundamental group are the same as local systems, we see that there must be a local system on
, and since representations of the fundamental group are the same as local systems, we see that there must be a local system on 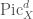 , and furthermore the sheaf
, and furthermore the sheaf 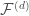 is the pullback of this local system. There is then an inductive method to extend this to
is the pullback of this local system. There is then an inductive method to extend this to 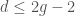 , and we can check that the local system is a character sheaf.
, and we can check that the local system is a character sheaf.
Now let us go back to our case of interest, the local Langlands correspondence. Instead of the curve  we will use
we will use 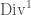 , the moduli of degree
, the moduli of degree 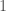 Cartier divisors. It will be useful to have an alternate description of
Cartier divisors. It will be useful to have an alternate description of 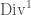 in terms of Banach-Colmez spaces.
in terms of Banach-Colmez spaces.
For any perfectoid space  over
over  and any vector bundle
and any vector bundle 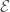 over
over 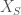 , the Banach-Colmez space
, the Banach-Colmez space 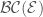 is the locally spatial diamond such that
is the locally spatial diamond such that 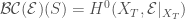 . We define
. We define 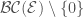 to be such that
to be such that 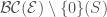 are the sections in
are the sections in 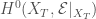 which are nonzero fiberwise on
which are nonzero fiberwise on  .
.
There is a map from 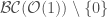 to
to 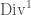 which sends a section
which sends a section 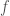 to
to 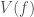 , which in turn induces an isomorphism
, which in turn induces an isomorphism  . A more explicit description of this map is given by Lubin-Tate theory (see also The Lubin-Tate Formal Group Law). After choosing a coordinate, the Lubin-Tate formal group law
. A more explicit description of this map is given by Lubin-Tate theory (see also The Lubin-Tate Formal Group Law). After choosing a coordinate, the Lubin-Tate formal group law 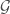 with an action of
with an action of 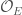 , over
, over 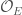 , is isomorphic to
, is isomorphic to ![\mathrm{Spf}(\mathcal{O}_{E}[[x]])](https://s0.wp.com/latex.php?latex=%5Cmathrm%7BSpf%7D%28%5Cmathcal%7BO%7D_%7BE%7D%5B%5Bx%5D%5D%29&bg=ffffff&fg=444444&s=0&c=20201002) . We can form the universal cover
. We can form the universal cover 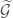 which is isomorphic to
which is isomorphic to ![\mathrm{Spf}(\mathcal{O}_{E}[[x^{1/q^{\infty}}]])](https://s0.wp.com/latex.php?latex=%5Cmathrm%7BSpf%7D%28%5Cmathcal%7BO%7D_%7BE%7D%5B%5Bx%5E%7B1%2Fq%5E%7B%5Cinfty%7D%7D%5D%5D%29&bg=ffffff&fg=444444&s=0&c=20201002) . Now let
. Now let 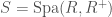 be a perfectoid space with tilt
be a perfectoid space with tilt 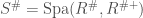 . We have
. We have  , where
, where 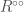 is the set of topologically nilpotent elements in
is the set of topologically nilpotent elements in  , and the map which sends a topologically nilpotent element
, and the map which sends a topologically nilpotent element  to the power series
to the power series ![\sum_{i}\pi^{i}[x^{q^{-i}}]](https://s0.wp.com/latex.php?latex=%5Csum_%7Bi%7D%5Cpi%5E%7Bi%7D%5Bx%5E%7Bq%5E%7B-i%7D%7D%5D&bg=ffffff&fg=444444&s=0&c=20201002) gives a map to
gives a map to 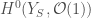 , which upon quotienting out by the action of Frobenius gives an isomorphism between
, which upon quotienting out by the action of Frobenius gives an isomorphism between 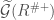 and
and 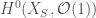 .
.
What this tells us is that ![H^{0}(X_{S},\mathcal{O}(1))\cong \mathrm{Spd}(\mathbb{F}[[x^{1/p^{\infty}}]])](https://s0.wp.com/latex.php?latex=H%5E%7B0%7D%28X_%7BS%7D%2C%5Cmathcal%7BO%7D%281%29%29%5Ccong+%5Cmathrm%7BSpd%7D%28%5Cmathbb%7BF%7D%5B%5Bx%5E%7B1%2Fp%5E%7B%5Cinfty%7D%7D%5D%5D%29&bg=ffffff&fg=444444&s=0&c=20201002) . Defining
. Defining  to be the completion of the union over all
to be the completion of the union over all 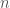 of the
of the 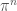 -torsion points of
-torsion points of 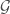 in
in  , we have that
, we have that  . This is an
. This is an 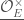 -torsor over
-torsor over 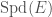 , and then quotienting out by the action of Frobenius we obtain our map to
, and then quotienting out by the action of Frobenius we obtain our map to 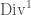 .
.
More generally, we have an isomorphism 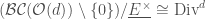 , where
, where 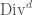 parametrized degree
parametrized degree 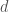 relative Cartier divisors on
relative Cartier divisors on  .
.
Now that we have our description of 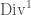 (and more generally
(and more generally 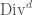 ) in terms of Banach-Colmez spaces, let us now see how we can translate the strategy of Deligne to the local case. Once again we have an Abel-Jacobi map
) in terms of Banach-Colmez spaces, let us now see how we can translate the strategy of Deligne to the local case. Once again we have an Abel-Jacobi map
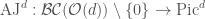
Given a local system on 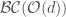 , we want to have a character sheaf on
, we want to have a character sheaf on 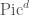 whose pullback to
whose pullback to 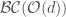 is precisely this local system. Again what our strategy hinges will be whether
is precisely this local system. Again what our strategy hinges will be whether 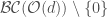 will be simply connected. And in fact this is true for
will be simply connected. And in fact this is true for  , and by a result called Drinfeld’s lemma for diamonds this will actually be enough to prove the local Langlands correspondence for
, and by a result called Drinfeld’s lemma for diamonds this will actually be enough to prove the local Langlands correspondence for  (i.e. it is not needed for
(i.e. it is not needed for 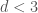 – in fact this is false for
– in fact this is false for  !). The fact that
!). The fact that 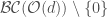 is simply connected for
is simply connected for  is a result of Fargues, and, at least for the characteristic
is a result of Fargues, and, at least for the characteristic  case, follows from expressing
case, follows from expressing ![\mathcal{BC}(\mathcal{O}(d))\setminus\lbrace 0\rbrace=\mathrm{Spa}(\mathbb{F}_{q}[[x_{1}^{1/p^{\infty}},\ldots,x_{d}^{1/p^{\infty}}]])\setminus V(x_{1},\ldots x_{d})](https://s0.wp.com/latex.php?latex=%5Cmathcal%7BBC%7D%28%5Cmathcal%7BO%7D%28d%29%29%5Csetminus%5Clbrace+0%5Crbrace%3D%5Cmathrm%7BSpa%7D%28%5Cmathbb%7BF%7D_%7Bq%7D%5B%5Bx_%7B1%7D%5E%7B1%2Fp%5E%7B%5Cinfty%7D%7D%2C%5Cldots%2Cx_%7Bd%7D%5E%7B1%2Fp%5E%7B%5Cinfty%7D%7D%5D%5D%29%5Csetminus+V%28x_%7B1%7D%2C%5Cldots+x_%7Bd%7D%29&bg=ffffff&fg=444444&s=0&c=20201002) , whose category of etale covers is the same as that of
, whose category of etale covers is the same as that of ![\mathrm{Spa}(\mathbb{F}_{q}[[x_{1},\ldots,x_{d}]])\setminus V(x_{1},\ldots x_{d})](https://s0.wp.com/latex.php?latex=%5Cmathrm%7BSpa%7D%28%5Cmathbb%7BF%7D_%7Bq%7D%5B%5Bx_%7B1%7D%2C%5Cldots%2Cx_%7Bd%7D%5D%5D%29%5Csetminus+V%28x_%7B1%7D%2C%5Cldots+x_%7Bd%7D%29&bg=ffffff&fg=444444&s=0&c=20201002) . Then Zariski-Nagata purity allows one to reduce this to showing that
. Then Zariski-Nagata purity allows one to reduce this to showing that ![\mathrm{Spa}(\mathbb{F}_{q}[[x_{1},\ldots,x_{d}]])](https://s0.wp.com/latex.php?latex=%5Cmathrm%7BSpa%7D%28%5Cmathbb%7BF%7D_%7Bq%7D%5B%5Bx_%7B1%7D%2C%5Cldots%2Cx_%7Bd%7D%5D%5D%29&bg=ffffff&fg=444444&s=0&c=20201002) is simply connected, which it is by Hensel’s lemma.
is simply connected, which it is by Hensel’s lemma.
VI. The Cohomology of Local Shimura Varieties
Many years before the work of Fargues and Scholze, the  case of the local Langlands correspondence (see also The Local Langlands Correspondence for General Linear Groups) was originally proven using the cohomology of the Lubin-Tate tower (which we shall denote by
case of the local Langlands correspondence (see also The Local Langlands Correspondence for General Linear Groups) was originally proven using the cohomology of the Lubin-Tate tower (which we shall denote by  ) which parametrizes deformations of the Lubin-Tate formal group law (see also The Lubin-Tate Formal Group Law) with level structure, together with the cohomology of Shimura varieties. Let us now investigate how the cohomology of the Lubin-Tate tower can be related to what we have just discussed.
) which parametrizes deformations of the Lubin-Tate formal group law (see also The Lubin-Tate Formal Group Law) with level structure, together with the cohomology of Shimura varieties. Let us now investigate how the cohomology of the Lubin-Tate tower can be related to what we have just discussed.
It turns out that because of the relationship between Lubin-Tate formal group laws, p-divisible groups, and vector bundles on the Fargues-Fontaine curve, the Lubin-Tate tower is also a moduli space of modifications of vector bundles on the Fargues-Fontaine curve, but of a very specific kind! Namely, it parametrizes modifications where we fix the two vector bundles, and furthermore one has to be the trivial bundle 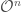 and the other a degree
and the other a degree 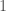 bundle
bundle 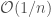 , and so the only thing that varies is the isomorphism between them (as opposed to the Hecke stack, where the vector bundles can also vary) away from a point. So we see that the Lubin-Tate tower is a part of the Hecke stack (we can think of it as the fiber of the Hecke stack above
, and so the only thing that varies is the isomorphism between them (as opposed to the Hecke stack, where the vector bundles can also vary) away from a point. So we see that the Lubin-Tate tower is a part of the Hecke stack (we can think of it as the fiber of the Hecke stack above 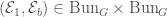 ).
).
More generally, the Lubin-Tate tower is a special case of a local Shimura variety at infinite level, which is itself related to a special case of a moduli stack of local shtukas. These parametrize modifications of  -bundles
-bundles 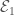 and
and 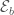 , which are bounded by some cocharacter
, which are bounded by some cocharacter 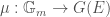 . This moduli stack of local shtukas, denoted
. This moduli stack of local shtukas, denoted 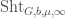 , is an inverse limit of locally spatial diamonds
, is an inverse limit of locally spatial diamonds 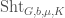 with “level structure” given by some compact open subgroup
with “level structure” given by some compact open subgroup  of
of  . In the case where the cocharacter
. In the case where the cocharacter 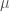 is miniscule, the data
is miniscule, the data  is called a local Shimura datum, and we define the local Shimura variety at infinite level, denoted
is called a local Shimura datum, and we define the local Shimura variety at infinite level, denoted 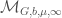 , to be such that
, to be such that 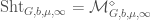 . It is similarly a limit of local Shimura varieties at finite level
. It is similarly a limit of local Shimura varieties at finite level  , denoted
, denoted 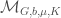 , and for each
, and for each  we have
we have 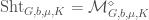 .
.
Let us now see how the cohomology of the moduli stack of local shtukas is related to our setup. We will consider the case of finite level, i.e. 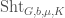 , since the cohomology at infinite level may be obtained as a limit. Consider the inclusion
, since the cohomology at infinite level may be obtained as a limit. Consider the inclusion ![j_{1}:[\ast/\underline{G(E)}]\hookrightarrow \mathrm{Bun}_{G}](https://s0.wp.com/latex.php?latex=j_%7B1%7D%3A%5B%5Cast%2F%5Cunderline%7BG%28E%29%7D%5D%5Chookrightarrow+%5Cmathrm%7BBun%7D_%7BG%7D&bg=ffffff&fg=444444&s=0&c=20201002) . Now consider the object
. Now consider the object 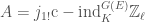 of
of 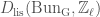 . Now for our cocharacter
. Now for our cocharacter 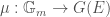 , we have a Hecke operator
, we have a Hecke operator 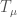 , and we apply this Hecke operator to obtain
, and we apply this Hecke operator to obtain 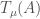 . Now we pull this back through the inclusion
. Now we pull this back through the inclusion ![j_{b}:[\ast/\underline{G_{b}(E)}]\hookrightarrow \mathrm{Bun}_{G}](https://s0.wp.com/latex.php?latex=j_%7Bb%7D%3A%5B%5Cast%2F%5Cunderline%7BG_%7Bb%7D%28E%29%7D%5D%5Chookrightarrow+%5Cmathrm%7BBun%7D_%7BG%7D&bg=ffffff&fg=444444&s=0&c=20201002) , to get an object
, to get an object 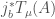 of
of  . We can think of all this happening not on the entire Hecke stack, but only on
. We can think of all this happening not on the entire Hecke stack, but only on 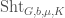 , since we are specifically only considering this very special kind of modification parametrized by
, since we are specifically only considering this very special kind of modification parametrized by 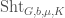 . But the derived pushforward from
. But the derived pushforward from 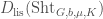 to a point gives
to a point gives 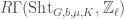 (from which we can compute the cohomology).
(from which we can compute the cohomology).
This relationship between the cohomology of the moduli stack of local shtukas and sheaves on 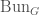 , as we have just discussed, has been used to obtain new results. For instance, David Hansen, Tasho Kaletha, and Jared Weinstein used this formulation together with the concept of the categorical trace to prove the Kottwitz conjecture.
, as we have just discussed, has been used to obtain new results. For instance, David Hansen, Tasho Kaletha, and Jared Weinstein used this formulation together with the concept of the categorical trace to prove the Kottwitz conjecture.
Let 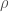 be a smooth irreducible representation of
be a smooth irreducible representation of  over
over 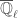 . We define
. We define
![\displaystyle R\Gamma(G,b,\mu)[\rho]=\varinjlim_{K\subset G(E)}R\mathrm{Hom}(R\Gamma_{c}(\mathrm{Sht}_{G,b,\mu,K},\mathcal{S}_{\mu}),\rho)](https://s0.wp.com/latex.php?latex=%5Cdisplaystyle+R%5CGamma%28G%2Cb%2C%5Cmu%29%5B%5Crho%5D%3D%5Cvarinjlim_%7BK%5Csubset+G%28E%29%7DR%5Cmathrm%7BHom%7D%28R%5CGamma_%7Bc%7D%28%5Cmathrm%7BSht%7D_%7BG%2Cb%2C%5Cmu%2CK%7D%2C%5Cmathcal%7BS%7D_%7B%5Cmu%7D%29%2C%5Crho%29&bg=ffffff&fg=444444&s=0&c=20201002)
Let 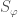 be the centralizer of
be the centralizer of 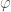 in
in 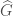 . Given a representation
. Given a representation  in the L-packet
in the L-packet 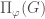 and a representation
and a representation 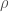 in the L-packet
in the L-packet 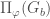 , the refined local Langlands correspondence gives us a representation
, the refined local Langlands correspondence gives us a representation 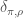 of
of 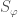 . We let
. We let 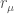 be the extension of the highest-weight representation of
be the extension of the highest-weight representation of 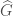 to
to  . The Kottwitz conjecture states that
. The Kottwitz conjecture states that
![\displaystyle R\Gamma(G,b,\mu)[\rho]=\sum_{\pi\in\Pi_{\varphi}(G)}\pi\boxtimes\mathrm{Hom}_{S_{\varphi}}(\delta_{\pi,\rho},r_{\mu}\circ \varphi)](https://s0.wp.com/latex.php?latex=%5Cdisplaystyle+R%5CGamma%28G%2Cb%2C%5Cmu%29%5B%5Crho%5D%3D%5Csum_%7B%5Cpi%5Cin%5CPi_%7B%5Cvarphi%7D%28G%29%7D%5Cpi%5Cboxtimes%5Cmathrm%7BHom%7D_%7BS_%7B%5Cvarphi%7D%7D%28%5Cdelta_%7B%5Cpi%2C%5Crho%7D%2Cr_%7B%5Cmu%7D%5Ccirc+%5Cvarphi%29&bg=ffffff&fg=444444&s=0&c=20201002)
The approach of Hansen, Kaletha, and Weinstein involve first using a generalized Jacquet-Langlands transfer operator 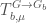 . We define the regular semisimple elements in
. We define the regular semisimple elements in  to be the semisimple elements whose connected centralizer is a maximal torus, and we define the strongly regular semisimple elements to be the regular semisimple elements whose centralizer is connected. We denote their corresponding open subvarieties in
to be the semisimple elements whose connected centralizer is a maximal torus, and we define the strongly regular semisimple elements to be the regular semisimple elements whose centralizer is connected. We denote their corresponding open subvarieties in  by
by 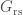 and
and 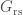 respectively. The generalized Jacquet-Langlands transfer operator
respectively. The generalized Jacquet-Langlands transfer operator 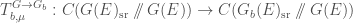 is defined to be
is defined to be
=\sum_{(g,g',\lambda)\in\mathrm{Rel}_{b}}f(g)\dim r_{\mu}[\lambda]](https://s0.wp.com/latex.php?latex=%5Cdisplaystyle+%5BT_%7Bb%2C%5Cmu%7D%5E%7BG%5Cto+G_%7Bb%7D%7Df%5D%28g%27%29%3D%5Csum_%7B%28g%2Cg%27%2C%5Clambda%29%5Cin%5Cmathrm%7BRel%7D_%7Bb%7D%7Df%28g%29%5Cdim+r_%7B%5Cmu%7D%5B%5Clambda%5D&bg=ffffff&fg=444444&s=0&c=20201002)
Here the set 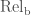 is the set of all triples
is the set of all triples 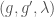 where
where 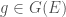 ,
, 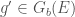 , and
, and 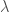 is a certain specially defined element of
is a certain specially defined element of  (
( being the centralizer of
being the centralizer of 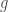 in
in  ) that depends on
) that depends on 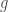 and
and  . When applied to the Harish-Chandra character
. When applied to the Harish-Chandra character 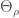 , we have
, we have
=\sum_{\pi\in\Pi_{\varphi}(G)}\dim \mathrm{Hom}_{S_{\varphi}}(\delta_{\pi,\rho},r_{\mu})\Theta_{\pi}(g)](https://s0.wp.com/latex.php?latex=%5Cdisplaystyle+%5BT_%7Bb%2C%5Cmu%7D%5E%7BG%5Cto+G_%7Bb%7D%7D%5CTheta_%7B%5Crho%7D%5D%28g%29%3D%5Csum_%7B%5Cpi%5Cin%5CPi_%7B%5Cvarphi%7D%28G%29%7D%5Cdim+%5Cmathrm%7BHom%7D_%7BS_%7B%5Cvarphi%7D%7D%28%5Cdelta_%7B%5Cpi%2C%5Crho%7D%2Cr_%7B%5Cmu%7D%29%5CTheta_%7B%5Cpi%7D%28g%29&bg=ffffff&fg=444444&s=0&c=20201002)
Next we have to relate this to the cohomology of the moduli stack of local shtukas. We first need the language of distributions. We define
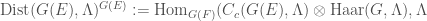
To any object  of
of 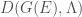 , we can associate an object
, we can associate an object 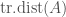 of
of 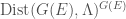 . We also have “elliptic” versions of these constructions, i.e. an object
. We also have “elliptic” versions of these constructions, i.e. an object 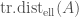 of the category
of the category 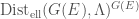 . Now we can define the action of the generalized Jacquet-Langlands transfer operator on
. Now we can define the action of the generalized Jacquet-Langlands transfer operator on 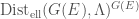 . The hope will be that we will have the following equality:
. The hope will be that we will have the following equality:
![\displaystyle T_{b,\mu}^{G\to G_{b}}\mathrm{tr.dist}_{\mathrm{ell}}\rho=\mathrm{tr.dist}_{\mathrm{ell}}R\Gamma(G,b,\mu)[\rho]](https://s0.wp.com/latex.php?latex=%5Cdisplaystyle+T_%7Bb%2C%5Cmu%7D%5E%7BG%5Cto+G_%7Bb%7D%7D%5Cmathrm%7Btr.dist%7D_%7B%5Cmathrm%7Bell%7D%7D%5Crho%3D%5Cmathrm%7Btr.dist%7D_%7B%5Cmathrm%7Bell%7D%7DR%5CGamma%28G%2Cb%2C%5Cmu%29%5B%5Crho%5D&bg=ffffff&fg=444444&s=0&c=20201002)
Proving this equality is where the geometry of 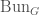 (and the Hecke stack) and the trace formula come into play. The action of the generalized Jacquet-Langlands transfer operator
(and the Hecke stack) and the trace formula come into play. The action of the generalized Jacquet-Langlands transfer operator 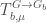 on
on 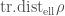 can be described in a similar way to a Hecke operator where we pull back to the moduli of local Shtukas, multiply by a kernel function, and then push forward.
can be described in a similar way to a Hecke operator where we pull back to the moduli of local Shtukas, multiply by a kernel function, and then push forward.
On the other side, one needs to compute ![\mathrm{tr.dist}_{\mathrm{ell}}R\Gamma(G,b,\mu)[\rho]](https://s0.wp.com/latex.php?latex=%5Cmathrm%7Btr.dist%7D_%7B%5Cmathrm%7Bell%7D%7DR%5CGamma%28G%2Cb%2C%5Cmu%29%5B%5Crho%5D&bg=ffffff&fg=444444&s=0&c=20201002) . Here we use that
. Here we use that ![R\Gamma(G,b,\mu)[\rho]=h_{\rightarrow *}'j^{*}(q^{*}\mathcal{S}_{\mu}\otimes h_{\leftarrow}^{*}i_{b *}\rho)](https://s0.wp.com/latex.php?latex=R%5CGamma%28G%2Cb%2C%5Cmu%29%5B%5Crho%5D%3Dh_%7B%5Crightarrow+%2A%7D%27j%5E%7B%2A%7D%28q%5E%7B%2A%7D%5Cmathcal%7BS%7D_%7B%5Cmu%7D%5Cotimes+h_%7B%5Cleftarrow%7D%5E%7B%2A%7Di_%7Bb+%2A%7D%5Crho%29&bg=ffffff&fg=444444&s=0&c=20201002) . This is a version of the expression of the cohomology of the moduli stack of local shtukas that we previously discussed where
. This is a version of the expression of the cohomology of the moduli stack of local shtukas that we previously discussed where 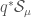 is the pullback to the Hecke stack of the sheaf corresponding to
is the pullback to the Hecke stack of the sheaf corresponding to 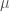 provided by the geometric Satake equivalence and before pushing forward via
provided by the geometric Satake equivalence and before pushing forward via 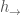 we are pulling back to the degree
we are pulling back to the degree 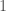 part of the Hecke stack, which is why we have
part of the Hecke stack, which is why we have 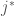 (the embedding of this degree
(the embedding of this degree 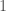 part) and
part) and 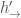 denotes that we are pushing forward from this degree
denotes that we are pushing forward from this degree 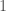 part.
part.
Hansen, Kaletha, and Weinstein then apply a categorical version of the Lefschetz-Verdier trace formula (using a framework developed by Qing Lu and Weizhe Zheng) to be able to relate ![\mathrm{tr.dist}_{\mathrm{ell}}R\Gamma(G,b,\mu)[\rho]=\mathrm{tr.dist}_{\mathrm{ell}}h_{\rightarrow *}'j^{*}(q^{*}\mathcal{S}_{\mu}\otimes h_{\leftarrow}^{*}i_{b *}\rho)](https://s0.wp.com/latex.php?latex=%5Cmathrm%7Btr.dist%7D_%7B%5Cmathrm%7Bell%7D%7DR%5CGamma%28G%2Cb%2C%5Cmu%29%5B%5Crho%5D%3D%5Cmathrm%7Btr.dist%7D_%7B%5Cmathrm%7Bell%7D%7Dh_%7B%5Crightarrow+%2A%7D%27j%5E%7B%2A%7D%28q%5E%7B%2A%7D%5Cmathcal%7BS%7D_%7B%5Cmu%7D%5Cotimes+h_%7B%5Cleftarrow%7D%5E%7B%2A%7Di_%7Bb+%2A%7D%5Crho%29&bg=ffffff&fg=444444&s=0&c=20201002) to
to 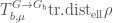 .
.
Let us discuss briefly the setting of this categorical trace. We consider a category 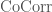 whose objects are pairs
whose objects are pairs  where
where  is an Artin v-stack over
is an Artin v-stack over  and
and 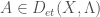 . The morphisms in this category are given by a pair of maps
. The morphisms in this category are given by a pair of maps  where
where 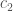 is smooth-locally representable in diamonds, together with a map
is smooth-locally representable in diamonds, together with a map 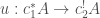 . We also write
. We also write  for the pair
for the pair 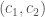 . Given an endomorphism
. Given an endomorphism 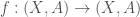 the categorical trace of
the categorical trace of 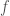 is given by
is given by 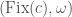 where
where 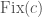 is the pullback of
is the pullback of 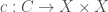 and
and 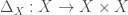 and
and 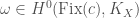 (here
(here 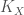 is the dualizing sheaf, which may obtained as the right-derived pullback of
is the dualizing sheaf, which may obtained as the right-derived pullback of  via the structure morphism of
via the structure morphism of  ). In the special case where the correspondence
). In the special case where the correspondence  arises form an automorphism
arises form an automorphism 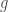 of
of  , and
, and  , then one may think of
, then one may think of 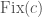 as the fixed points of
as the fixed points of 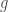 and the categorical trace gives an element of
and the categorical trace gives an element of  (the local term) for each fixed point.
(the local term) for each fixed point.
For Hansen, Kaletha, and Weinstein’s application, they consider 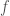 to be the identity. The categorical trace is then given by
to be the identity. The categorical trace is then given by 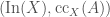 , where
, where 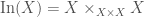 is the inertia stack, classifying pairs
is the inertia stack, classifying pairs 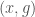 with
with 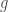 an automorphism of
an automorphism of  , and
, and  is called the characteristic class.
is called the characteristic class.
The idea now is that certain properties of the setting we are considering (such as universal local acyclicity) allow us to identify the trace distribution 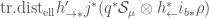 as a characteristic class
as a characteristic class 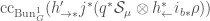 . From there we can use properties of the abstract theory to relate it to
. From there we can use properties of the abstract theory to relate it to 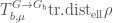 (for instance, we can use a Kunneth formula for the characteristic class to decouple the parts involving
(for instance, we can use a Kunneth formula for the characteristic class to decouple the parts involving 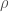 and
and 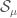 , and relate the former to pulling back to the moduli stack of local shtukas, and relate the part involving the latter to multiplication by the kernel function).
, and relate the former to pulling back to the moduli stack of local shtukas, and relate the part involving the latter to multiplication by the kernel function).
VII. The Spectral Action
We have seen that the machinery of excursion operators gives us the automorphic to Galois direction of the local Langlands correspondence. We now describe one possible approach to obtain the other (Galois to automorphic) direction. We are going to use the language of the categorical geometric Langlands correspondence mentioned at the end of in The Global Langlands Correspondence for Function Fields over a Finite Field.
Recall our construction of the moduli stack of local 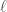 -adic Galois representations in Moduli Stacks of Galois Representations. Using the same strategy we can construct a moduli stack of L-parameters, which we shall denote by
-adic Galois representations in Moduli Stacks of Galois Representations. Using the same strategy we can construct a moduli stack of L-parameters, which we shall denote by  . This notation comes from the fact that in Fargues and Scholze’s work the L-parameters can be viewed as 1-cocycles.
. This notation comes from the fact that in Fargues and Scholze’s work the L-parameters can be viewed as 1-cocycles.
Let  denote the subcategory of compact objects in
denote the subcategory of compact objects in  . The categorical local Langlands correspondence in this case is the following conjectural equivalence of categories:
. The categorical local Langlands correspondence in this case is the following conjectural equivalence of categories:
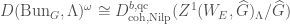
Here the right-hand side is the derived category of bounded complexes on 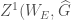 with quasicompact support, coherent cohomology, and nilpotent singular support. We will leave the definition of these terms to the references, but we will think of
with quasicompact support, coherent cohomology, and nilpotent singular support. We will leave the definition of these terms to the references, but we will think of  as being a derived category of coherent sheaves on
as being a derived category of coherent sheaves on 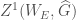 .
.
We now outline an approach to proving the categorical local Langlands correspondence. Let 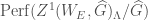 be the category of perfect complexes on
be the category of perfect complexes on  . Then there is an action of
. Then there is an action of 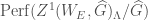 on
on 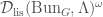 , called the spectral action, such that composing with the map
, called the spectral action, such that composing with the map 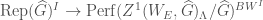 gives us the action of the Hecke operator.
gives us the action of the Hecke operator.
The idea is that the spectral action gives us a functor from 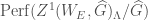 to
to 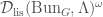 , sending an object
, sending an object 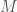 of
of 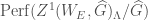 to the object
to the object  of
of 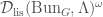 , where
, where  is the Whittaker sheaf (the sheaf on
is the Whittaker sheaf (the sheaf on 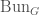 corresponding to the representation
corresponding to the representation 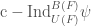 , where
, where 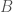 is a Borel subgroup of
is a Borel subgroup of  ,
, 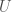 is the unipotent radical of
is the unipotent radical of 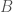 , and
, and  is a character of
is a character of 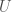 ). The hope is then that this functor can be extended from
). The hope is then that this functor can be extended from 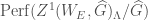 to all of
to all of  , and that it will provide the desired equivalence of categories.
, and that it will provide the desired equivalence of categories.
Now we discuss how this spectral action is constructed. Let us first consider the following more general situation. Let 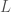 be a field of characteristic
be a field of characteristic 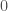 , let
, let  be a split reductive group, and let
be a split reductive group, and let 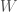 be a discrete group. We write
be a discrete group. We write 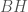 and
and 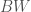 for their corresponding classifying spaces. Let
for their corresponding classifying spaces. Let  be an idempotent-complete,
be an idempotent-complete, 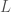 -linear stable
-linear stable 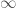 -category.
-category.
For all 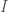 , a
, a 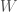 -equivariant, exact tensor action of
-equivariant, exact tensor action of  on
on  is a functor
is a functor
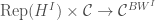
natural in 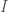 , exact as an action of
, exact as an action of  after forgetting the
after forgetting the 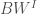 -equivariance, and such that the action of
-equivariance, and such that the action of 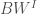 is compatible with the tensor product.
is compatible with the tensor product.
Now what we want to show is that a 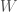 -equivariant, exact tensor action of
-equivariant, exact tensor action of  on
on  is the same as an
is the same as an 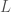 -linear action of
-linear action of 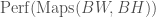 on
on  .
.
To prove the above statement, Fargues and Scholze use the language of higher category theory. Let  be the
be the 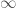 -category of anima, which is obtained from simplicial sets by inverting weak equivalences. The specific anima that we are interested in is
-category of anima, which is obtained from simplicial sets by inverting weak equivalences. The specific anima that we are interested in is 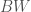 , which is obtained by taking the nerve of the category
, which is obtained by taking the nerve of the category ![[\ast/W]](https://s0.wp.com/latex.php?latex=%5B%5Cast%2FW%5D&bg=ffffff&fg=444444&s=0&c=20201002) . An important property of
. An important property of  is that it is freely generated under sifted colimits by the full subcategory of finite sets.
is that it is freely generated under sifted colimits by the full subcategory of finite sets.
We now define two functors 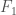 and
and 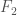 from
from 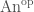 to
to  . The functor
. The functor 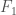 sends a finite set
sends a finite set  to the exact
to the exact 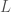 -linear actions of
-linear actions of  on
on  , which is equivalent to the exact
, which is equivalent to the exact 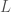 -linear monoidal functors from
-linear monoidal functors from  to
to  . The functor
. The functor 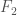 sends a finite set
sends a finite set  to the
to the  -equivariant exact actions of
-equivariant exact actions of  on
on  , which is equivalent to natural transformations from the functor
, which is equivalent to natural transformations from the functor  to the functor
to the functor 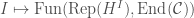 .
.
There is a natural transformation from 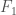 to
to 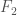 that happens to be an isomorphism on finite sets. Now since the category
that happens to be an isomorphism on finite sets. Now since the category  is generated by finite sets under sifted colimits, all we need is for the functors
is generated by finite sets under sifted colimits, all we need is for the functors 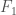 and
and 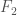 to preserve sifted colimits.
to preserve sifted colimits.
For 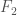 this follows from the fact that
this follows from the fact that 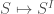 preserves sifted colimits. For
preserves sifted colimits. For 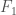 , this comes from the fact that
, this comes from the fact that ![\mathrm{Maps}(S,BH)\cong [\mathrm{Spec}(A)/H^{S'}]](https://s0.wp.com/latex.php?latex=%5Cmathrm%7BMaps%7D%28S%2CBH%29%5Ccong+%5B%5Cmathrm%7BSpec%7D%28A%29%2FH%5E%7BS%27%7D%5D&bg=ffffff&fg=444444&s=0&c=20201002) for some animated
for some animated 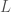 -algebra
-algebra  and some set
and some set 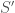 , and then looking at the structure of
, and then looking at the structure of ![\mathrm{Perf}([\mathrm{Spec}(A)/H^{S'}])](https://s0.wp.com/latex.php?latex=%5Cmathrm%7BPerf%7D%28%5B%5Cmathrm%7BSpec%7D%28A%29%2FH%5E%7BS%27%7D%5D%29&bg=ffffff&fg=444444&s=0&c=20201002) and
and ![\mathrm{IndPerf}([\mathrm{Spec}(A)/H^{S'}])](https://s0.wp.com/latex.php?latex=%5Cmathrm%7BIndPerf%7D%28%5B%5Cmathrm%7BSpec%7D%28A%29%2FH%5E%7BS%27%7D%5D%29&bg=ffffff&fg=444444&s=0&c=20201002) .
.
Now that we have our abstract theory let us go back to our intended application. Let 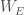 be the Weil group of
be the Weil group of 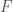 . It turns out that every L-parameter
. It turns out that every L-parameter 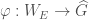 factors through a quotient
factors through a quotient 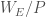 , where
, where  is some open subgroup of the wild inertia. This means that
is some open subgroup of the wild inertia. This means that 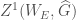 is the union of all
is the union of all 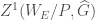 over all such
over all such  (compare also with the construction in Moduli Stacks of Galois Representations), and this also means that we can focus our attention on
(compare also with the construction in Moduli Stacks of Galois Representations), and this also means that we can focus our attention on 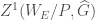 .
.
We can actually go further and replace 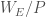 with its subgroup
with its subgroup 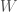 generated by the elements
generated by the elements  and
and  satisfying
satisfying 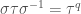 , together with the wild inertia (we have also already considered this in Moduli Stacks of Galois Representations, where we called it
, together with the wild inertia (we have also already considered this in Moduli Stacks of Galois Representations, where we called it 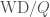 ), and get the same moduli space, i.e.
), and get the same moduli space, i.e. 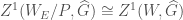 .
.
Let 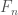 be the free group on
be the free group on 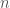 generators. For every map
generators. For every map 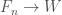 , we have a map
, we have a map
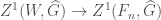
The category 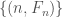 is a sifted category, and upon taking sifted colimits, we obtain an isomorphism
is a sifted category, and upon taking sifted colimits, we obtain an isomorphism
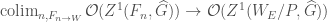
There is also a version of this statement that involves higher category theory. It says that the map
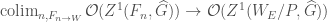
is an isomorphism in the stable 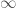 -category
-category  . Furthermore the category
. Furthermore the category 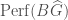 generates
generates 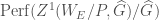 under cones and retracts, and
under cones and retracts, and 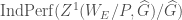 identifies with the
identifies with the 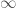 -category of
-category of  -modules inside
-modules inside  .
.
If we take invariants under the action of 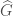 , we then have
, we then have
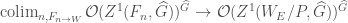
Note that  is precisely the same data as the algebra of excursion operators. We can see this using the fact that
is precisely the same data as the algebra of excursion operators. We can see this using the fact that 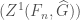 is isomorphic to
is isomorphic to 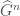 , and
, and 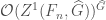 is functions on
is functions on 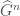 which are invariant under the action of
which are invariant under the action of  . But this is the same as the data of an excursion operator
. But this is the same as the data of an excursion operator 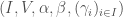 (
( here has
here has  elements), because such a function is of the form
elements), because such a function is of the form  .
.
Now that we have our description of 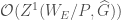 as
as  , we can now apply the abstract theory developed earlier to obtain our spectral action.
, we can now apply the abstract theory developed earlier to obtain our spectral action.
Let us now focus on the case of 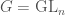 and relate the spectral action to the more classical language of Hecke eigensheaves (see also The Global Langlands Correspondence for Function Fields over a Finite Field). Let
and relate the spectral action to the more classical language of Hecke eigensheaves (see also The Global Langlands Correspondence for Function Fields over a Finite Field). Let 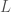 be an algebraically closed field over
be an algebraically closed field over 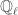 . Given an L-parameter
. Given an L-parameter 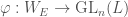 , we have an inclusion
, we have an inclusion 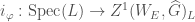 and a sheaf
and a sheaf  on
on 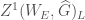 . For any
. For any 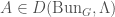 we can take the spectral action
we can take the spectral action 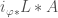 . This turns out to be a Hecke eigensheaf! However, it is often going to be zero. Still, in work by Johannes Anschütz and Arthur-César Le Bras, they show that the above construction can give an example of a nonzero Hecke eigensheaf, by relating the spectral action to an averaging functor, which is an idea that comes from the work of Edward Frenkel, Dennis Gaitsgory, and Kari Vilonen on the geometric Langlands program.
. This turns out to be a Hecke eigensheaf! However, it is often going to be zero. Still, in work by Johannes Anschütz and Arthur-César Le Bras, they show that the above construction can give an example of a nonzero Hecke eigensheaf, by relating the spectral action to an averaging functor, which is an idea that comes from the work of Edward Frenkel, Dennis Gaitsgory, and Kari Vilonen on the geometric Langlands program.
VIII. The p-adic local Langlands correspondence
The work of Fargues and Scholze deals with the “classical” (i.e. 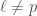 ) local Langlands correspondence. As we have seen for example in Completed Cohomology and Local-Global Compatibility, the p-adic local Langlands correspondence (i.e.
) local Langlands correspondence. As we have seen for example in Completed Cohomology and Local-Global Compatibility, the p-adic local Langlands correspondence (i.e. 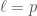 ) is much more complicated and mysterious compared to the classical case. Still, one might wonder whether the machinery we have discussed here can be suitably modified to obtain an analogous “geometrization” of the p-adic local Langlands correspondence.
) is much more complicated and mysterious compared to the classical case. Still, one might wonder whether the machinery we have discussed here can be suitably modified to obtain an analogous “geometrization” of the p-adic local Langlands correspondence.
Since we are dealing with what we might call p-adic, instead of 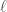 -adic, Galois representations, we would have to replace
-adic, Galois representations, we would have to replace 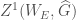 with the moduli stack of
with the moduli stack of 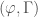 -modules (also known as the Emerton-Gee stack, see also Moduli Stacks of (phi, Gamma)-modules).
-modules (also known as the Emerton-Gee stack, see also Moduli Stacks of (phi, Gamma)-modules).
We still would like to work with the derived category of some sort of sheaves on 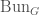 . This is because, in work of Pierre Colmez, Gabriel Dospinescu, and Wieslawa Niziol (and also in related work of Peter Scholze which uses a different approach), the p-adic etale cohomology of the Lubin-Tate tower has been used to realize the p-adic local Langlands correspondence, and we have already seen that the Lubin-Tate tower is related to
. This is because, in work of Pierre Colmez, Gabriel Dospinescu, and Wieslawa Niziol (and also in related work of Peter Scholze which uses a different approach), the p-adic etale cohomology of the Lubin-Tate tower has been used to realize the p-adic local Langlands correspondence, and we have already seen that the Lubin-Tate tower is related to 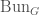 and the Hecke stack. Since p-adic etale cohomology is the subject of p-adic Hodge theory (see also p-adic Hodge Theory: An Overview), we might also expect ideas from p-adic Hodge theory to become relevant.
and the Hecke stack. Since p-adic etale cohomology is the subject of p-adic Hodge theory (see also p-adic Hodge Theory: An Overview), we might also expect ideas from p-adic Hodge theory to become relevant.
So now have to find some sort of p-adic replacement for 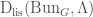 . It is believed that the correct replacement might be the derived category of almost solid modules, whose theory is currently being developed by Lucas Mann. Some of the ideas are similar to that used by Peter Scholze to formulate p-adic Hodge theory for rigid-analytic varieties (see also Rigid Analytic Spaces), but also involves many new ideas. Let us go through each of the meanings of the words in turn.
. It is believed that the correct replacement might be the derived category of almost solid modules, whose theory is currently being developed by Lucas Mann. Some of the ideas are similar to that used by Peter Scholze to formulate p-adic Hodge theory for rigid-analytic varieties (see also Rigid Analytic Spaces), but also involves many new ideas. Let us go through each of the meanings of the words in turn.
The “almost” refers to theory of almost rings and almost modules developed by Gerd Faltings (see also the discussion at the end of Adic Spaces and Perfectoid Spaces). For an  -module
-module 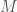 over a local ring
over a local ring  , we say that
, we say that 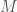 is almost zero if it is annihilated by some element of the maximal ideal of
is almost zero if it is annihilated by some element of the maximal ideal of  . We define the category of almost
. We define the category of almost  -modules (or
-modules (or  -modules) to be the category of
-modules) to be the category of  -modules modulo the category of almost zero modules.
-modules modulo the category of almost zero modules.
The “solid” refers to the theory of solid rings and solid modules discussed earlier, although we will use the later language developed by Dustin Clausen and Peter Scholze. Let  be a ring. We define the category of condensed
be a ring. We define the category of condensed  -modules, denoted
-modules, denoted 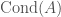 , to be the category of sheaves of
, to be the category of sheaves of  -modules on the category of profinite sets. Given a profinite set
-modules on the category of profinite sets. Given a profinite set 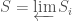 , we define
, we define ![A_{\blacksquare}[S]](https://s0.wp.com/latex.php?latex=A_%7B%5Cblacksquare%7D%5BS%5D&bg=ffffff&fg=444444&s=0&c=20201002) to be the limit
to be the limit ![\varinjlim_{A'}\varprojlim_{i}A'[S_{i}]](https://s0.wp.com/latex.php?latex=%5Cvarinjlim_%7BA%27%7D%5Cvarprojlim_%7Bi%7DA%27%5BS_%7Bi%7D%5D&bg=ffffff&fg=444444&s=0&c=20201002) , where
, where 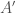 runs over all finite-type
runs over all finite-type  -algebras contained in
-algebras contained in  , and we define the category of solid
, and we define the category of solid  -modules, denoted
-modules, denoted  , to be the subcategory of
, to be the subcategory of 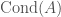 generated by
generated by ![A_{\blacksquare}[S]](https://s0.wp.com/latex.php?latex=A_%7B%5Cblacksquare%7D%5BS%5D&bg=ffffff&fg=444444&s=0&c=20201002) . The idea of condensed mathematics is to incorporate topology – for instance the category of compactly generated weak Hausdorff spaces, which forms most of the topological spaces we care about, embeds fully faithfully into the category of condensed sets. On the other hand, condensed abelian groups, rings, modules, etc. have nice algebraic properties, for instance when it comes to forming abelian categories, which topological abelian groups, rings, modules, etc. do not have. The solid rings and solid modules corresponds to “completions”, and in particular they have a reasonable “completed tensor product” that will become useful to us later on when forming derived categories.
. The idea of condensed mathematics is to incorporate topology – for instance the category of compactly generated weak Hausdorff spaces, which forms most of the topological spaces we care about, embeds fully faithfully into the category of condensed sets. On the other hand, condensed abelian groups, rings, modules, etc. have nice algebraic properties, for instance when it comes to forming abelian categories, which topological abelian groups, rings, modules, etc. do not have. The solid rings and solid modules corresponds to “completions”, and in particular they have a reasonable “completed tensor product” that will become useful to us later on when forming derived categories.
Finally, the “derived category” refers to the same idea of a category of complexes with morphisms up to homotopy and quasi-isomorphisms inverted, as we have previously discussed, except, however, that we need to actually not completely forget the homotopies; in fact we need to remember not only the homotopies but the “homotopies between homotopies”, and so on, and for this we need to formulate derived categories in the language of infinity category theory. The reason why we need to this is because our definition will involve “gluing” derived categories, and for this we need to remember the homotopies, including the higher ones.
Let us now look at how Mann constructs this derived category of almost solid modules. Let  be the category of affinoid perfectoid spaces
be the category of affinoid perfectoid spaces 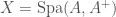 together with a pseudouniformizer
together with a pseudouniformizer  of
of  . We define a functor
. We define a functor 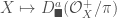 as the sheafification of the functor
as the sheafification of the functor 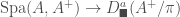 (the derived category of almost solid
(the derived category of almost solid 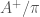 -modules) on
-modules) on  equipped with the pro-etale topology.
equipped with the pro-etale topology.
If 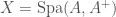 is weakly perfectoid of finite type over some totally disconnected space, then
is weakly perfectoid of finite type over some totally disconnected space, then 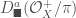 is just
is just  . More generally,
. More generally,  will gave a pro-etale cover by some
will gave a pro-etale cover by some  which is weakly perfectoid of finite type over some totally disconnected space, and
which is weakly perfectoid of finite type over some totally disconnected space, and 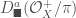 can be expressed as the limit
can be expressed as the limit 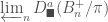 , where
, where 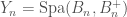 , and
, and  runs over is the degree
runs over is the degree 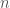 part of the Cech nerve of
part of the Cech nerve of  .
.
Now let  be a small v-stack. There is a unique hypercomplete (this means it satisfies descent along all hypercovers, which are generalizations of the Cech nerve) sheaf on
be a small v-stack. There is a unique hypercomplete (this means it satisfies descent along all hypercovers, which are generalizations of the Cech nerve) sheaf on  that agrees with the functor
that agrees with the functor 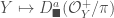 for every affinoid perfectoid space
for every affinoid perfectoid space  in
in  . We define
. We define 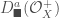 to be the global sections of this sheaf. This is the construction that we want to apply to
to be the global sections of this sheaf. This is the construction that we want to apply to  .
.
The derived category of almost solid modules comes with a six-functor formalism (see also Perverse Sheaves and the Geometric Satake Equivalence). Let 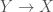 be a map. The derived pullback
be a map. The derived pullback 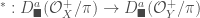 is the restriction map of the sheaf
is the restriction map of the sheaf  . The derived pushforward
. The derived pushforward 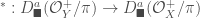 is defined to be the right adjoint to the derived pullback. The derived tensor product
is defined to be the right adjoint to the derived pullback. The derived tensor product  and derived Hom
and derived Hom  are inherited from
are inherited from  .
.
The remaining two functors in the six-functor formalism are the “shriek” functors 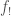 and
and 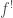 . If
. If 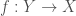 is a “nice” enough map, we have a factorization of
is a “nice” enough map, we have a factorization of 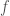 into a composition
into a composition  where
where 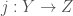 is etale and
is etale and 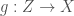 is proper, and we define
is proper, and we define

where 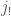 is the right-adjoint to
is the right-adjoint to 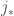 . We then define
. We then define  to be the right-adjoint to
to be the right-adjoint to 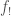 . The six-functor formalism satisfies certain important properties, such as functoriality of
. The six-functor formalism satisfies certain important properties, such as functoriality of 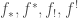 , proper base change for
, proper base change for 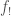 , and a projection formula for
, and a projection formula for 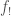 . In Lucas Mann’s thesis, he uses the six-functor formalism he has developed to prove Poincare duality for a rigid-analytic variety
. In Lucas Mann’s thesis, he uses the six-functor formalism he has developed to prove Poincare duality for a rigid-analytic variety  of pure dimension
of pure dimension 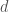 over an algebraically closed nonarchimedean field
over an algebraically closed nonarchimedean field  of mixed characteristic:
of mixed characteristic:

As of the moment, there are still many questions regarding a possible geometrization of the p-adic local Langlands program. As more developments are worked out, we hope to be able to discuss them in future posts on this blog, together with the different aspects of the theory that has already been developed, and the many other different future directions that it may lead to.
References:
Geometrization of the Local Langlands Correspondence by Laurent Fargues and Peter Scholze
Geometrization of the Local Langlands Program (notes by Tony Feng from a workshop at McGill University)
The Geometric Langlands Conjecture (notes from Oberwolfach Arbeitsgemeinschaft)
Berkeley Lectures on p-adic Geometry by Peter Scholze and Jared Weinstein
Etale Cohomology of Diamonds by Peter Scholze
On the Kottwitz Conjecture for Local Shtuka Spaces by David Hansen, Tasho Kaletha, and Jared Weinstein
Averaging Functors in Fargues’ Program for GL_n by Johannes Anschütz and Arthur-César Le Bras
Cohomologue p-adique de la Tour de Drinfeld: le Cas de la Dimension 1 by Pierre Colmez, Gabriel Dospinescu, and Wiesława Nizioł
A p-adic 6-Functor Formalism in Rigid-Analytic Geometry by Lucas Mann
Lectures on Condensed Mathematics by Peter Scholze
Report from Oberwolfach from totallydisconnected
subvarieties!
, where
is a squarefree positive integer, i.e.
is a real quadratic field. We denote its ring of integers by
. The group
acts on the product
of two upper half-planes as follows:
, where
are the Galois conjugates of
. If we then take the left quotient of
by this action of
, we then end up with a complex analytic surface
, which is non-compact. Just as the “open” modular curve constructed in The Moduli Space of Elliptic Curves parametrizes elliptic curves over
, the open modular surface
which we have just constructed parametrizes abelian surfaces
over
with an extra “real multiplication” structure, which is an embedding of
into their ring of endomorphisms
.
(note that
is also equipped with an action of
), which adds a finite number (equal to the class number of
) of points called cusps. This compactification, which we denote
, will be singular. However, by the theory developed by Heisuke Hironaka, there is a way to “resolve” the singularities, and by applying this theory we may obtain a smooth projective surface
.
is a meromorphic function
on
such that, for
, we have
be a more general totally real field, instead of just a real quadratic field. This leads to the more general notion of a Hilbert modular variety, and of more general Hilbert modular forms. We also note that instead of
, we could instead consider some nontrivial level structure
, where
is some fractional ideal of
. The group
is defined to be the group of matrices of the form
where
,
, and
.
. However there is another way to describe them via the exceptional isomorphisms of spin groups (which are double covers of special orthogonal groups, see also Rotations in Three Dimensions) with other groups – In our case, we have the isomorphism
. Let us discuss first the general theory behind spin groups of signature
and their associated symmetric spaces, and then later we apply it to the specific case of Hilbert modular surfaces.
be a pair consisting of a vector space
over
and a quadratic form
. The orthogonal group
is the subgroup of the group of linear transformations of
which preserve
. The Clifford algebra
associated to
is the quotient of the tensor algebra of
by the relation, for all
,
and
) and Hamilton’s quaternions for
and
. Note that, unlike the complex numbers, more general Clifford algebras such as Hamilton’s quaternions have more than one type of “conjugation”. The first, which we shall call
, is induced by negation of basis elements of
. Another is given by cyclically permuting the tensor factors of an element so that
for
. This second conjugation allows us to define the Clifford norm:
of
is the subalgebra generated by elements which are a product of an even number of basis elements of
. The odd part
is similarly defined, and we have the decomposition
. The Clifford group is defined to be the set of all invertible elements
of the Clifford algebra such that
. The intersection of the even Clifford algebra and the Clifford group is called
. The set of elements of
whose Clifford norm is equal to
is called
.
has dimension
that we will use later when we discuss Hilbert modular surfaces again. Let
be a basis of
such that
for all
. Let
. The center
of the Clifford algebra associated to
is then isomorphic to
, and the even Clifford algebra admits the description
such that
and for
let
. We define the new vector space
to be the set of all elements
of
such that the automorphism
agrees with the conjugation
, and we equip
with the quadratic form
. It turns out that
is isometric to
, and the upshot is that we can now describe the action of an element
on an element
as follows:
.
, and may be obtained as the quotient of
by its locally compact subgroup
. We want to generalize this to the group
, but it is often useful to have different descriptions of the symmetric space. We will discuss three different descriptions of the symmetric space on which
acts, each one with its own advantages and disadvantages.
-dimensional subspaces of a vector space. It is a generalization of projective space (which is the special case when
). In our case, we want to parametrize
-dimensional spaces of
, with the additional condition that the quadratic form
is positive definite on this space:
acts on
, and the stabilizer of an element
is a maximal compact subgroup
, which is isomorphic to
. Therefore we can see that
, and provides a realization of its associated symmetric space. However, in this model it is harder to see the complex analytic structure.
be the complexification of
and define
is an
-dimensional complex manifold consisting of two connected components. We choose one of these components and denote it by
– this is our symmetric space. Although the complex analytic structure is easier to see in the projective model, it is hard to relate this model to well-known examples of symmetric spaces such as the upper half-plane (which is the case when
).
be a nonzero isotropic vector in
and let
be another vector in
such that
. We let
be the intersection of the orthogonal complements of
and
in
, so that
, the restriction of the quadratic form
has signature
. We let
denote the complexification of
and define
and
by sending
to
. We denote the preimage of
by
– the latter is analogous to the upper half-plane.
be a lattice in
. The idea is that if we pick a vector
in the dual lattice
in
, and consider the orthogonal complement of
in
, what we get is actually a vector space of signature
, to which we can once again apply the preceding constructions! Applied to the case of Hilbert modular surfaces, this explains the embedded modular curves. In symbols, we have
, then we can also describe
in the tube domain model as follows:
as the sum of all the
where
satisfies the condition that
. We can further define the composite Heegner divisor
as half the sum of all Heegner divisors
as
runs over
.
-dimensional vector space
, equipped with the quadratic form
. We choose the following basis for
:
, and the even Clifford algebra
of
is of the form
. Via the assignments
and
. Furthermore, the Clifford norm on
corresponds to the determinant on
. All in all, this gives us an isomorphism between
and
. The theory we have discussed earlier provides us with the following vector space
isomorphic to
:
and
as matrices inside
as follows:
, we also have
. In turn this gives us an isomorphism
.
where
is the discriminant of
are also known as Hirzebruch-Zagier divisors. They have the explicit description
such that
. As a special case,
is the modular curve of level
(i.e. the compactified moduli space of elliptic curves).